Parabol Çözümlü Sorular ve Formüller

LYS sınavına hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Parabol online soru çözümleri yapan gözde hocaların Parabol çözümlü sorular videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak anlatım yapanlara göre derleyerek aşağıya matematik Parabol cevaplı sorular videolarını listeledik, Değerli okuyucumuz aşağıda LYS matematik 2 konuları içinde yer alan online matematik Parabol online çözümlü örnekleri istediğiniz hocayı seçerek izleyebilirsiniz. Ayrıca Videoların devamında da matematik Parabol formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Soru Çözüm videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)Matematik Parabol Çözümlü Sorular Videolar

Sitemizde Aşağıda yer alan Matematik Parabol soru çözümleri gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Parabol canlı çözümlü örneklerin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır.

Matematik Parabol Formüller

A. TANIM

olmak üzere,tanımlanan f(x) = ax2 + bx + c biçimindeki fonksiyonlara ikinci dereceden bir değişkenli fonksiyonlar denir.

İkinci dereceden fonksiyonun analitik düzlemdeki görüntüsüne parabol denir.Parabol, düzgün tel parça-sının uçlarından tutularak bükülmesiyle oluşan, yandaki gibi kolları yukarıya doğru ya da aşağıya doğru olan bir eğridir.

 

B. PARABOLÜN TEPE NOKTASI

1) f(x) = ax² + bx + c fonksiyonunun tepe noktası

T(r, k) olmak üzere,

r= (-b/2a)  ve k= f(r) = (4ac-b²)/4a dır.

bunlar biliniyorsa f(x) = a.(x−r)² + k parabol denklemi yazılabilir

Parabol  x= (-b/2a) doğrusuna göre simetriktir.

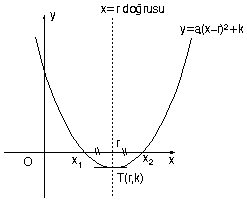
x= (-b/2a) doğrusu parabolün simetri eksenidir.

y = a(x – r)2 + k fonksiyonunun grafiğinin tepe noktası T(r, k) dır.

C. GRAFİĞİN EKSENLERİ KESTİĞİ NOKTALAR

Parabolün Ox eksenini kestiği noktalar A ve B, Oy eksenini kestiği nokta C olsun.

ax² + bx + c = 0 ın kökleri x1 ve x2 ise A(x₁, 0), B(x₂, 0), C(0, c) dir.

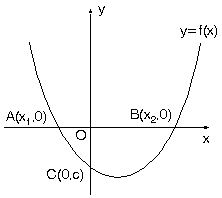
ax² + bx + c = 0 denkleminde

• D = b² – 4ac > 0 ise, parabol Ox eksenini farklı iki noktada keser.
• D = b² – 4ac < 0 ise, parabol Ox eksenini kesmez.
• D = b² – 4ac = 0 ise, parabol Ox eksenine teğettir.

 

D. x² NİN KATSAYISI OLAN a NIN İŞARETİ

1)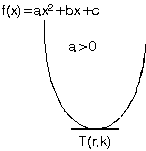

a>0 ise parabolün kolları yukarı doğru olup,f(x),in en küçük değeri tepe noktasının ortinatı olan k dır.

2) a < 0 ise, parabolün kolları aşağı doğru olup, f(x) in en büyük değeri tepe noktası-nın ordinatı olan k dır.

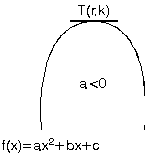.a>0 ise parabolün kolları aşağı doğru olup f(fx) in en büyük değeri tepe noktasının ortinatı olan k dır.

3) |a| büyüdükçe kollar daralır. Buna göre, yandaki parabollere göre, f deki x2 nin katsayısı, g deki x2 nin katsayısından büyüktür.

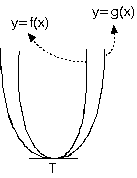|a| büyüdükçe kollar daralır. Buna göre , yandaki parabollere göre ,f deki x2 nin katsayısı g deki x2 nin katsayısından büyüktür

f(x) = ax² + bx + c fonksiyonunun grafiğini çizmek için,

1) Fonksiyonun tepe noktası bulunur.

2) Fonksiyonun eksenleri kestiği noktalar bulunur.

3) a nın işaretine bakılarak parabolün kollarının yönü belirlenir.

E. GRAFİĞİ VERİLEN PARABOLÜNDENKLEMİNİN YAZILMASI

1. Parabolün Ox Eksenini Kestiği Noktalar Biliniyorsa

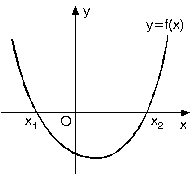y = f(x) = a(x – x₁) (x – x₂) … (1) dir.

Burada a değerini bulmak için, parabol üzerindeki herhangi bir noktanın değerleri (1) de yazılır.

2. Parabolün Tepe Noktası Biliniyorsa

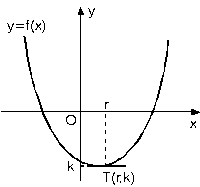y = f(x) = a(x – r)² + k … (1) dir.

Burada a değerini bulmak için, parabol üzerindeki herhangi bir noktanın değerleri (1) de yazılır.

3. Parabolün Geçtiği Üç Nokta Biliniyorsa

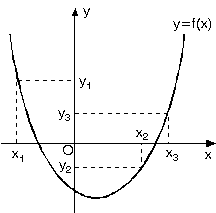y₁ = ax₁² + bx₁ + c … (1)

y₂ = ax₂² + bx₂ + c … (2)

y₃ = ax₃² + bx₃ + c … (3)

Bu üç denklemi ortak çözerek a, b, c yi buluruz.

F. PARABOL İLE DOĞRUNUNDÜZLEMDEKİ DURUMU

y = f(x) = ax² + bx + c parabolü ile y = g(x) = mx + n doğrusunu ortak çözelim.

f(x) = g(x)

ax² + bx + c = mx + n

ax² + (b – m)x + c – n = 0 … (_*)

(_*) denkleminin kökleri (varsa) doğru ile parabolün kesiştiği noktaların apsisleridir.

Buna göre, (_*) denkleminde;

•  D > 0 ise, parabol doğruyu farklı iki noktada keser.
•   D< 0 ise, parabol ile doğru kesişmez.
•  D = 0 ise, parabol doğruya teğettir.

y = ax² + bx + c parabolü ile y = dx² + ex + f parabolünün düzlemdeki durumu incelenirken yukarıdakine benzer biçimde işlemler yapılır.

Burada bulunan Matematik Parabol Çözümlü Sorular videolarından, Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizide yorum alanından bize iletebilirsiniz.

[egit1]
[egit2]
[egit3]