Egitim-Dünyası

Karmaşık Sayılar Çözümlü Sorular ve Formüller

Karmaşık Sayılar Çözümlü Sorular ve Formüller

LYS sınavına hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Karmaşık Sayılar online soru çözümleri yapan gözde hocaların Karmaşık Sayılar çözümlü sorular videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak anlatım yapanlara göre derleyerek aşağıya matematik Karmaşık Sayılar cevaplı sorular videolarını listeledik, Değerli okuyucumuz aşağıda LYS matematik 2 konuları içinde yer alan online matematik Karmaşık Sayılar online çözümlü örnekleri istediğiniz hocayı seçerek izleyebilirsiniz. Ayrıca Videoların devamında da matematik Karmaşık Sayılar formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Soru Çözüm videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)Matematik Karmaşık Sayılar Çözümlü Sorular Videolar

Şenol Hocaİbrahim HocaNejdet hocaHalit HocaKarışıkÇıkmış SorularMatematik Karmaşık Sayılar Konu Anlatımları VideoDiğer
Matematik Karmaşık Sayılar Çözümlü Sorular Şenol Hoca

Matematik Karmaşık Sayılar Çözümlü Sorular İbrahim Hoca

Matematik Karmaşık Sayılar Çözümlü Sorular Nejdet hoca

Matematik Karmaşık Sayılar Çözümlü Sorular Halit hoca

Matematik Karmaşık Sayılar Çözümlü Sorular

Matematik Karmaşık Sayılar Çözümlü Sorular (Çıkmış Sorular) Ekol Hoca

Matematik

Karmaşık Sayılar

KONU ANLATIMI DERS İZLE
[t1]
[t2]
Sitemizde yukarıda yer alan Matematik Karmaşık Sayılar soru çözümleri gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Karmaşık Sayılar canlı çözümlü örneklerin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır.

Matematik Karmaşık Sayılar Formüller

Karmaşık Sayılar, Özellikleri, Karmaşık Sayılarda İşlemler

a,b ∈ R ve i2= −1 olmak üzere Z = a + bi biçiminde tanımlı Z sayısına karmaşık (kompleks) sayı denir. Karmaşık sayılar kümesi C ile gösterilir. Z = a + bi karmaşık sayısında;
1) a’ya Z nin gerçel (reel) kısmı (Re(Z) = a) denir.
2) b’ye Z nin sanal (imajiner) kısmı (Im(Z) = b) denir.

√−1 = i
√−a = √(−1).a = √a.i
i1 = i
i2 =−1
i3 =−i
i4 = 1
i4n+1 = i
i4n+2 =−1
i4n+3 =−i
i4n = 1

Bir Karmaşık Sayının Eşleniği

Z = a + bi karmaşık sayısı için 11_karmaşık-sayılar = a − bi sayısına Z nin eşleniği denir. [Z = 2 + 3i ise 11_karmaşık-sayılar = 2 − 3i]

Karmaşık Sayılarda İşlemler
Z1 = a + bi ve Z2= c + di karmaşık sayıları için:
1) (a = c) ve (b = d) ise Z1 = Z2 dir.
2) Z1± Z2 = (a±c) + (b±d)i
3) Z1.11_karmaşık-sayılar2 = (a+bi).(c+di) = (ac-bd) + (ad+bc)i
4) Z1.Z1 = a2 + b2
5) Z1/Z2=(Z1.11_karmaşık-sayılar2)/(Z2.11_karmaşık-sayılar2)=(ac+bd)/(c2+d2) + (bc − ad)i/(c2 + d2)

Karmaşık Sayıların Kutupsal Gösterimi – Karmaşık Sayılarda Argüment

Karmaşık Sayıların Kutupsal Biçimde Gösterimi – Karmaşık Sayılarda Argüment


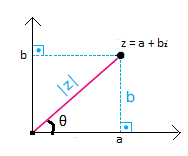
r =|Z|=|OZ|= √(a²+b²)

reel sayısına Z nin mutlak değeri (modülü) denir.

a) |z|=|11_karmaşık-sayılar|=|-z|

b) |z1.z2|=|z1|.|z2|

c) |z|.|11_karmaşık-sayılar| = |z|2

d) |z1n|= (|z1|)n

e)1

θ sayısına z karmaşık sayısının esas argümenti denir ve Arg(z) = θ ile gösterilir. Yukarıdaki dik üçgende;

2

3

olduğuna göre;

4

5

biçiminde yazılabilir. Buna z’nin kutupsal biçimi denir.

Kutupsal Gösterimin Özellikleri

z1 =|z1|(Cosθ + i.Sinθ) ve z2 =|z2|(Cosα + iSinα) ise:

1) -z1 =|z1|. [Cos(∏+θ) + iSin(∏+θ)]

2)z1 =|z1|. [Cos(2.∏-θ) + iSin(2.∏-θ)]

3) z1 . z2 =|z1|.|z2|[Cos(θ+α) + iSin(θ+α)]

4) z1n =|z1|n . (Cosnθ + iSinnθ)

Karmaşık Sayıların Kökleri

5)6   

6)7

Buna göre z nin kare kökleri:

8

9

Karmaşık Sayıların Geometrik Özellikleri

1) |z – (a+b)i|= r denklemi analitik düzlemde merkezi M(a,b) ve yarıçapı r olan çember denklemidir.

2) |z – (a+b)i|< r ifadesi merkezi M(a,b) ve yarı çapı r olan çemberin iç bölgesidir.

3) |z – (a+b)i|> r ifadesi merkezi M(a,b) ve yarıçapı r olan çemberin dış bölgesidir.

4) |z₁+z₂|≤|z₁|+|z₂|

Burada bulunan Matematik Karmaşık Sayılar Çözümlü Sorular videolarından, Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizide yorum alanından bize iletebilirsiniz.

[egit1]
[egit2]
[egit3]

ZİYARETÇİ YORUMLARI

Henüz yorum yapılmamış. İlk yorumu aşağıdaki form aracılığıyla siz yapabilirsiniz.

BİR YORUM YAZ