Yüzde Problemleri Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Yüzde Problemleri online ders anlatımı yapan gözde hocaların Yüzde Problemleri konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Yüzde Problemleri video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik Yüzde Problemleri konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Yüzde Problemleri konusu ile ilgili yazılı anlatım ve genel Yüzde Problemleri formülleri de eklenmiştir.

Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen  yukarısında alt alta yer almaktadır.)Yüzde Problemleri Konu Anlatımı Videolar

Sitemizde Aşağıda yer alan Matematik Yüzde Problemleri Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Yüzde Problemleri canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.

Matematik Yüzde Problemleri Konu Anlatımı Yazılı

 

1/4 kesrini biliyorsunuz değil mi? Daha önce karsılaşmamış olamazsınız. Peki, bir sayının 1/4’ünü bulmayı biliyor musunuz? Sanırım onu da biliyorsunuzdur.

”4’e bölerim, yani 1/4 ile çarparım, biter!” diyorsunuzdur. Doğru!

Peki, paydasında 4 olan birkaç kesri birbiriyle toplamayı, çıkarmayı, çarpmayı ve bölmeyi biliyor musunuz? Buna da mı evet?

O halde ”1/4” nasıl okunur, onu çoktan biliyorsunuzdur. Büyük ihtimalle “Bir bölü dört”, kalan küçük ihtimalle de “dörtte bir” diye okuyorsunuzdur.

İkisi de doğrudur. İste paydasında ”4” yazan kesirler ”Dörtte bilmem kaç” diye okunduğundan, böyle problemlere dörtte problemleri demekte ben bir mahzur görmüyorum.

Aynı bunun gibi, paydasında 100 bulunan kesirlerle ilgili problemlere de yüzde problemleri denir.

Anlayacağınız dörtte problemleriyle problemi olmayan bir vatandasın yüzde problemleriyle de problemi olamaz, olmamalı. Varsa, birileri bu insana ”yüzde 25” ile ”dörtte bir” arasında hiçbir farkın olmadığını anlatmalı!

Ben buna aday oldum ama bakalım başarabilecek miyim?

1/4 kesrinin pay ve paydasını 25 ile genişletelim:

1/4 = 25/100. Simdi bu kesri okuyalım: ”25 bölü 100” veya “yüzde 25”. Biz ikinci okunuşu benimsiyor ve yazım kolaylığı olsun diye “%25” seklinde yazıyoruz. Diğer herkes gibi.

%25 olayının, anlayacağınız 1/4 olayından hiçbir farkı yok. ”Farkı yoksa neden hiçbir kitapta dörtte problemleri yok da yüzde problemleri var?” diye aklınıza bir soru gelmiş olabilir.

Açıklayayım:

A, B, C, D, E’nin bulunduğu bir grupta C, B’den 2 cm. uzun, D, A’dan 3 cm. kısa, B, E’den 1 cm. uzun ve C, D’den 5 cm. kısadır.

Simdi söyleyin bakalım, kim en uzun, kim en kısa, kim ortanca, anlayabildiniz mi? İlk okuyuşta hepsini sıraya dizebildiğinize ihtimal vermiyorum.

Yoksa elinizdeki bu notlarla isiniz olmazdı.

Bir de şunu dinleyin:

A, B, C, D, E’nin bulundugu bir grupta, A, B, C, D sırasıyla E’den 11, 1, 3, 8 cm. uzundur.

Simdi en uzun kim, en kısa kim, ortanca kim? Hepinizin simdi daha çabuk doğru cevabı bulduğunuza dair bahse girebilirim. Bu, su götürmez bir gerçektir. Yani, herkesin birbiriyle kıyaslanması yerine herkesin tek bir kişiye göre kıyaslanması çoğu zaman, belki de her zaman, daha anlaşılırdır.

Burada A’ya kıyas noktası diyebiliriz. Hocam niye A alınmış, B alınsaydı olmaz mıydı? Olurdu, ama o zaman da niye B alınmış derdiniz siz.

Kesirli ifadelerde de kıyas noktası 100 olarak alınmış.

4 alınmamış, napalım!

Bir şeyin büyüklüğünü, kıyas noktası alarak açıklamanın ne kadar faydalı olduğuna dair bir başka örnek daha vereyim:

A sayısının 17/21’i mi daha büyüktür yoksa 162/199’u mu? Bunu da hemen hatasız bir şekilde doğru söylemiş olamazsınız. Hâlbuki ”A sayısının %83’ü mü daha büyüktür yoksa %82’si mi?” diye sorsaydık sanırım cevabınızı hem daha hızlı, hem de kesin bir doğrulukta verebilecektiniz.

Başka bir örnek daha verelim:

A ve B adında iki kişinin ikisi de 6 kilo vermişse, hangisinin daha çok zayıfladığına karar vermek mümkün olamaz.

Her ikisinin de zayıflamadan önce kaçar kilo olduklarını bilmemiz lazım veya ne bileyim başka bir bilgi gerek. Fakat bu bilgi bize ”A ve B yaptıkları rejim sonucunda toplam kilolarının sırasıyla %10 ve %15’ini kaybetmişlerdir” diye verilseydi, B’nin daha çok zayıfladığını rahatlıkla söyleyebilirdik.

Örnekleri çoğaltmak mümkün:

A insanı kumarda 100 lira, B insanı ise 10 lira kaybetmişse, sizce kim daha çok üzülmüştür? Elbet bunu cevaplamanın da mümkünatı yoktur.

Çünkü 10 lira kaybedenin belki tüm varı yoğu 10 liraydı, onu da kaybetmiş olabilir. Diğer yandan 100 lira kaybeden de belki bir milyarderdi. Olamaz mı? Ama ”A kumarda parasının %1’ini, B ise %100’ünü kaybetmiştir” deseydi, daha anlaşılır olurdu.

İste olayları, karları, zararları böyle yüzdeli ifadelerle anlatmak, daha anlaşılır olmamızı ve kıyaslamayı daha doğru şekilde yapmamızı sağlar.

Simdi ufak ufak yüzdeli sayılarla işlemlerin nasıl yapıldığına dair bilgiler vereceğiz.

Temel Yüzde İfadeleri:

Nasıl ki bir sayının 1/4’ü sorulduğunda sayıyı 4’e bölüyoruz yani 1/4 ile çarpıyoruz, bir sayının %25’i sorulduğunda da 25/100 ile çarpacağız.

Bir x sayısının

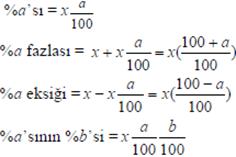
Örnekler

.

Tabii ki bazen bu işlemleri kısaltmak mümkün.

Örneğin, bir sayının %50’sini bulmak için 50/100 ile çarpmak, bir matematikçiye yakışmaz. 50/100 bizim sözlüğümüzde 1/2’ye eşittir.

Bir sayının %50’sini bulmak için yarısını almak yeter.

%20 = 1/5, %25 = 1/4 eşitliklerini bilmek de tabii ki daha hızlı olmamızı sağlar. Bunun gibi, %10 demek de 1/10 demek olduğundan bir sayının %10’u sorulduğunda 10’a bölsek yeter. %30’u sorulduğunda da

ve bir sayının 10’a bölünmesi çok kolay olduğundan, %30’u sorulan sayının önce 10’a bölünüp sonra 3 ile çarpılması da yeter.

Bununla birlikte; “x’in yüzde y’si” ile “y’nin yüzde x’i” ifadeleri eşdeğerdir. Çünkü biri

Diğeri dedür.

Bunu bilmek de çoğu zaman bize avantaj sağlatır. Mesela, 50’nin %4’ü yerine 4’ün %50’sini yani yarısını alırız, 2 olur biter!

Herhangi bir sayının basına % işareti konulduğunda sonucun değişmemesi için sayının 100 ile çarpılması gerekir.

Örneğin; 1/4 sayısının basına % sembolü yazılacaksa, 1/4’ü 100 ile çarpmak gerekir:

1/4 = %(1/4).100 = %25.

O halde, a = %100.a olacağını söyleyebiliriz. Hatta buradan

%100 = 1

eşitliğine bile ulaşırız.

Hani isçi/havuz problemlerinde de isin/havuzun %100’ü bittiğinde/dolduğunda, isler toplamını 1’e eşitlememizin temel sebebi buydu.

eşitliğinde, içler dışlar çarpımı da yapılabilir.

O halde yüzdeli ifadeleri orantılarda da kullanabileceğimizi anlarız.

Örnek: %20’si 60 olan sayı kaçtır?

Çözüm: Üç farklı şekilde çözeceğiz. İlk ikisinde orantı, üçüncüsünde denklem kuracağız.

Birinci yol: %20 ifadesi, 1/5 kesrine eşit olduğundan

1/5’i 60 ise

5/5’i x’dir.

x = 300

Bir sayı ile o sayının %a’sı doğru orantılı olduğundan içler-dışlar çarpımını eşitledik.

Yüzdeyi kesre çevirdiğimiz için bu metoda kesirli orantı kurma metodu diyeceğiz.

İkinci yol: Yine orantı kuracağız ama bu sefer kesre çevirmeden yüzdelerle ilsem yapacağız.

Tüm yollar içinde bu yol daha iyi gibi görünüyor.

Dikkatle inceleyiniz.

% 20’si 60 ise

%100’ü x’dir.

x = 300

Üçüncü yol: Denklem kurup, onu çözeceğiz. Aradığımız sayı x olsun. x’in %20’si 60’a eşit olduğundan

eşitliği geçerlidir. Dolayısıyla

x = 300 olur.

Örnek: A sayısı, B sayısının % kaç katıdır?

Çözüm: Nasıl ki 6 sayısı, 2 sayısının 6/2 = 3 katıdır, A sayısı da B sayısının A/B katı olur.

Hani bir sayıyı yüzdeli yazmak istiyorsak, 100 ile çarpıp önüne % işareti koyardık ya, o halde A sayısı B sayısının %(A/B).100 katıdır.

Hatta buna kısaca A sayısı, B sayısının %(100A/B)’sidir denir.

Örneğin;

1 sayısı, 4’ün %(1/4)100 = %25’i

4 sayısı, 1’in %400’ü

80 sayısı, 100’ün %(80/100)100 = %80’i

80 sayısı, 20’nin %(80/20)100 = %400’ü

20 sayısı, 100’ün %(20/100)100 = %20’si.

Uyarı:

i. 100 sayısı, 20’den %80 fazladır.

ii. 100 sayısı, 20’nin %400 fazlasıdır. ifadelerinden hangisi doğrudur?

Büyük çoğunluğunuz hemen ilk ifade doğru, ikinci ifade yanlış diyecektir. Hâlbuki iki ifade de yanlıştır.

100 sayısı 20’den 80 fazladır. %80 değil.

%80’iyse bile kimin %80’i? Bu belli değil. İkinci ifadede ise kaçtan 20’nin %400 fazlası kadar fazla olduğu belirtilmemiş. Bu sorunlar su sözler kullanılarak giderilmelidir:

“100 sayısı, 20’den 100’e göre %80 fazladır.”

“100 sayısı, 20’den 20’ye göre %400 fazladır.”

Örnek: A sayısı, B sayısının, B’ye göre % kaç fazlasıdır?

Çözüm: Önce yüzde olarak değil de sayı olarak kaç fazlası, onu bulalım. A sayısı B sayısının A – B fazlasıdır. B’ye göre kıyaslama sorulduğundan fazlalığı B’ye böleceğiz.

A – B fazlalığı B’nin

Örnek: A sayısı, B sayısından, A’ya göre % kaç fazladır?

Çözüm: Bu sefer, A’ya göre dediği için B’ye değil, A’ya böleceğiz. A – B fazlalık, A’nın

Örnek: Bir sınıfta 36 kız, 44 erkek öğrenci vardır. Kız öğrenciler sınıfın % kaçıdır?

Çözüm: Sınıfta 44 + 36 = 80 öğrenci vardır. Sınıftaki kızların sınıftaki öğrenci sayısına oranı 36/80‘dir. Yani 80 kişide 36 kişisi kız anlamına gelir.

Birinci yol: Sınıfın kız yüzdesi

İkinci yol:

80 kişilik sınıfta 36 kız varsa 100 kişilik sınıfta x kız olur

x = 45

Demek ki; kız öğrenci sayısı sınıfın %45’iymis.

Örnek: 20 erkek, 5 kız öğrencinin bulunduğu bir sınıfta,

a) Erkek öğrenci sayısı, kız öğrenci sayısının yüzde kaçıdır?

b) Kız öğrenci sayısı, erkek öğrenci sayısının yüzde kaçıdır?

c) Erkek öğrenci sayısı, sınıf mevcudunun yüzde kaçıdır?

d) Kız öğrenci sayısı, sınıf mevcudunun yüzde kaçıdır?

e) Erkek öğrenci sayısı kızların sayısının, kızlara göre % kaç fazlasıdır?

f) Erkek öğrenci sayısı, kızların sayısının, erkeklere göre % kaç fazladır?

Çözüm: 20 erkek ve 5 kız olduğundan sınıf mevcudu 25’tir.

a) 20 erkek, 5 kız öğrencinin %(20/5)100 = %400’üdür.

b) 5 kız, 20 erkek öğrencinin %(5/20)100 = %25’idir.

c) 20 erkek, 25 sınıf mevcudunun % (20/25)100

= %80’idir.

d) 5 kız, 25 sınıf mevcudunun %(5/25) 100 = %20’sidir.

e) 15 erkek fazla, kızlara göre bu fazlalık %(15/5)100 = %300’dür.

f) 15 erkek fazla, erkeklere göre bu fazlalık %(15/20)100 = %75’dir.

Örnek: Bir sınıftaki öğrencilerin %60’ı erkek, kalanı kızdır. Bu sınıftan erkek öğrencilerin %20’si ayrıldığında kalan erkek öğrenciler kız öğrencilerin % kaçı olur?

Çözüm: Yine üç farklı çözüm sunacağız.

Birinci yol: Değer verme yöntemi dediğimiz bu metot, en yaygın kullanılan metottur. En büyük kümenin eleman sayısı 100 gibi düşünülür. Niye 90 değil de 100 düşündünüz demiyorsunuz, değil mi?

48 erkek, 40 kızın %(48/40)100 = %120’si olduğundan cevabımız 120 olmalı. Garip gelmesin başlangıçta 60 erkek, 40 kızın %150’siydi.

İkinci yol: Yüzdeli hesabı kullanacağız.

%60 erkek ve %40 kızdan oluşan bir sınıf varmış.

%60 erkekten %20’si = %60.(20/100) = %12 ayrılmış.

%60 – %12 = %48 erkek kalmış. Kalan %48 erkekler, %40 olan kızların, %48

%120’si kadar olur.

Üçüncü yol: Yine denklem kuracağız. Sınıf mevcudu x olsun. Erkeklerin sayısı, sınıf mevcudunun %60’ı olduğundan

Kızların sayısı,

Erkeklerin %20’si ayrıldığından, %80’i kalmıştır.

Kalan erkek sayısı:

Bu da kızların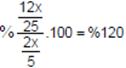‘sidir.

Bu üçüncü yol kullanılacaksa x yerine 100x gibi değer verilmesi yukarıdaki işlemlerinizi daha hızlı yapmanızı sağlayacaktır. İlerleyen bölümlerde örnek gösterilecektir.

Değer Verme Yöntemi.

Yüzdesi istenen ifadelere 100 değeri verilmesi kolaylık sağlayabilir (Ama 1/3’ünden bahsediliyorsa inatla da 100 vermeyin, 300 verin mesela. Tabii ki bulduğunuz cevabı 3’e bölmek kaydıyla).

Örnek: Buğdaydan ağırlığının %80’i kadar un, undan da ağırlığının %50 fazlası kadar hamur elde edilebilmektedir. Buna göre 360 kg. hamur elde etmek için kaç kg. buğday gereklidir?

Çözüm: 100 kg. buğdayımızın olduğunu düşünün. O halde bu kadar buğdaydan 80 kg. un çıkar. Simdi una su katıp hamur yapacağız. Hamur’unun %50 fazlası oluyormuş, yani 80 kg. undan 120 kg. hamur olur.

Sonuç olarak 100 kg. buğdaydan 120 kg. hamur çıktı. O zaman kaç kg. buğdaydan 360 kg. hamur çıkar diye bir doğru orantı kurarsak cevabın 300 kg. olması gerektiğini görürüz.

Örnek: Her zaman gittiği sabit yolda, hızını %25 arttıran bir araç, bu yolun sonuna her zamankine göre % kaç daha erken varır?

Çözüm: x = Vt eşitliğini unutmadınız umarım. Soruda hız %25 arttığından ve süredeki % azalmayı sorduğundan bu değişimleri kolay gözlemlemek amacıyla hız ve süreye 100 diyelim.

O halde x = 100.100 = 10000 km.dir. Hız %25 artarsa 125 km/s olur, yol değişmediğine göre;

10000 = 125.t eşitliğini kurar ve 100’lük sürenin 80’e düştüğünü görürüz. Geçen süre 100’den 80’e düştüğü için %20 daha erken vardığını söyleyebiliriz.

Örnek: Hızını %20 azaltıp, gideceği yolu %20 arttıran bir hareketli kullandığı süredeki değişim ilk duruma göre % kaçtır?

Çözüm: Simdi de hız ve yola 100 değerlerini verelim, buradan süredeki değişimi gözlemleyelim bakalım. Yine x = Vt eşitliğine başvuracağız.

100= 100.t₁ olduğundan ilk hikayeye göre süre 1 çıktı.

Simdi ikinci hikayeye geçelim: 120 = 80.t₂ eşitliğinden t₂ = 1,5 çıkar.

Sürenin 1’den 1,5’a çıkması 100’ün 150’ye çıkması gibi, yani ilk duruma göre 50 artma olduğundan süre %50 artmıştır.

Örnek: Hızını %20 arttırıp, gideceği yolu %20 azaltan bir hareketli kullandığı süredeki değişim ilk duruma göre % kaçtır?

Çözüm: Yine hız ve yola 100 değerlerini verelim, buradan süreyi gözlemleyelim.

İlk hikayeye göre 100 = 100.t₁ olduğundan ilk hikayeye göre süre 1 çıktı.

Simdi ikinci hikayeye geçelim: 80 = 120.t₂ eşitliğinden t₂ = 2/3 çıkar.

Sürenin 1’den 2/3’e düşmesi 300’ün 200’e yani 100’ün 200/3’e düşmesi anlamına gelir ki sürede ilk duruma göre 100 – 200/3 = 100/3 azalma olduğundan cevabımız %100/3 olur.

Örnek: Bir dikdörtgenin kısa kenarları %20 küçültülüp, uzun kenarları %20 arttırılarak bir dikdörtgen elde ediliyor. Dikdörtgenin alanındaki değişim % kaçtır?

Çözüm: A = ab olduğundan A = 100 olması için a = 10, b = 10 alalım.

Dikdörtgenin kısa kenarı 10 br. uzun kenarı 10 br olsa alanı 100 birim kare olur.

Son durumda kenarları 8 ve 12 br. Olduğundan alanı 8.12 = 96 birim kare olur.

İlk duruma göre 4 birim karelik bir azalma olmuştur.

O halde alandaki azalış %4 olmuştur.

Örnek: Bir dörtgenin tüm kenarları %20 arttırıldığında çevresi, ilk duruma göre % kaç artmıştır?

Çözüm: Ç = a + b + c + d olduğundan Ç = 100 olması için a = b = c = d = 25 br alalım.

Son durumda a = b = c = d = 25.120/100 = 30 br olduğundan Ç = 120 br. olur.

Yani %20 artış olmuştur.

Sonuç:

Bir toplamı oluşturan her terim %x arttırılırsa/azaltılırsa, toplamın sonucu da %x artar/azalır.

Soru. 1 + 2 + 3 + … + n toplamındaki her terim %10 arttırılırsa, toplamın sonucu % kaç artar?

Cevap: Üstteki sonuca güvenelim: %10. İnanmayanlar deneyebilir!

Örnek: Bir dikdörtgenin kısa kenarları %20 azaltıldığında alanın değişmemesi için uzun kenarlar % kaç arttırılmalıdır?

Çözüm: Yine a = b = 10 birim seçebiliriz. Eskiden alan 100’dü o zaman. Simdi iki kenarı 8’er birim oldu, alanın değişmemesi için diğer iki kenarı 12,5’ar birim olmalı. 10’dan 12,5’a çıkmak, %25 artmak manasına gelir.

Örnek: Bir eşkenar üçgenin kenarlarından biri %20 arttırılıyor, bir diğeri %20 azaltıldığında çevresindeki değişim % kaçtır?

Çözüm: a = b = c, Ç = a + b + c ve artırma ile azaltma eşit oranda olduğundan son durumda çevrede bir değişim olmaz. Fakat iki kenar uzunluğu arttırılıp, sadece tek kenar uzunluğu azaltılsaydı değişirdi.

Örnek: Bir dairenin yarıçapı %30 artarsa, alanı % kaç artar?

Çözüm: Alandaki değişmeyi kolay tayin edebilmek için, alanın 100’ün katı olması amacıyla dairenin yarıçapı 10 birim alalım.

Eski alan bu durumda 100 olur. Yarıçap %30 artarsa 13 birim olur.

O halde yeni alan 169 olur ki bu da alanın %69 arttığı anlamına gelir.

Örnek: Bir karenin her kenarı aynı oranda arttırılarak alanının %96 artması sağlanmıştır. Bu durumda çevresi % kaç artmıştır?

Çözüm: Bir sayının %96 artmasına aklınıza ilk gelen örnek 100’ün 196 olmasıdır. Yani eski alan 100 iken yeni alan 196 olmuş gibi düşünebiliriz.

Bu da eskiden karenin bir kenarının 10 birim iken simdi 14 birim olduğunu söyler. Yani karenin kenarlarını %40’ar arttırmışlar.

Kenarlardaki eşit artış oranı çevreye aynen yansırdı.

O halde çevresi %40 artmıştır.

Örnek: Fiyatlarda %10 indirim yapan bir mağazanın satışlarında %10 artış olduğuna göre mağazanın ilk duruma göre kar zarar durumu % kaçtır?

Çözüm: Kazanılan para = Birim fiyat × Satılan mal adedi olduğundan ilk durumdaki kazanılan paranın 100 olması için, birim fiyat 10, satılan miktar 10 olsun.

Son durumda birim fiyat 9, satılan mal miktarı 11 olur.

Kazanılan para 9.11= 99 olmuştur ki ilk duruma göre %1 azalmıştır.

%’deli Hesap Yöntemi:

%100 = 1 ve % = 1/100 anlamında olduğundan % sembolü olduğu gibi dört işlemde kullanılabilir.

a – b = a.%100 – b.%100 = (a – b).%100 = 100.%(a – b) en uygun biçimi elde edilerek soruların çözümünde kolaylık sağlamak mümkün olacak diye düşünüyorum.

a = %a.100 = a.%100 = 100.%a olacağını unutmayalım.

Örnek: %2.%50 = %%100 = %1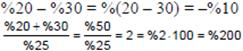

Örnek: x’in %20’si, y’nin %60’ına eşitse x, y’nin yüzde kaçıdır?

Çözüm: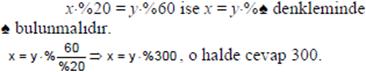

Örnek: x’in yüzde y’si 0,4 olduğuna göre x.y kaçtır?

Çözüm: x.%y = 0,4 => x.y = 40.

Örnek: 0,2’nin yüzde x’i 24 olduğuna göre x’in yüzde 1’i kaçtır?

Çözüm:

Sorulan: x. %1 = %x = ?

Verilen: 0,2.%x = 24 ise %x =120

Örnek: x’in yüzde y’si 5, y çarpımının %x’i 20 olduğuna göre x kaçtır?

Çözüm: x.%y = 5, x.y.%x = 20 taraf tarafa bölünürse x = 4 bulunur.

Örnek: %20’si kız olan bir sınıfa 10 kız öğrenci daha gelirse, sınıftaki erkek öğrenci oranı %64 oluyor. Erkek öğrenci sayısı kaçtır?

Çözüm: Sınıftaki kız oranı = Kız sayısı / Mevcut olduğunu hatırlayalım.

Mevcut = x = x.%100 olsun.

Erkek sayısı = x.%80 = Aranan sayı,

Son durumda kız oranı =

Örnek: Uzunlukları toplamı 20 cm olan iki farklı doğru parçasının uzunluklarından biri %10 artırılıp, diğeri %10 azaltıldığında elde edilen doğru parçalarının uzunlukları farkı 12 cm. oluyor.

Doğru parçalarının uzunlukları toplamı ilk duruma göre % kaç artmıştır?

Çözüm: a + b = 20 cm ve a > b olsun.

Son durumdaki artış:

a.%10 – b.%10 = 12.%10

Örnek: Bir dikdörtgenin kenarlarından biri %20 azaltılıp, diğeri %10 arttırılarak oluşturulan dikdörtgenin alanındaki değişim % kaçtır?

Çözüm: başlangıçta alan %100 kabul edilirse (%100 = 1), %20 azalan kenar %80 olur.

%10 artan kenar % 110 olur. Son Alan = %(%80).olur.

Bu da ilk duruma göre alan %12 azalır.

Bulunma Oranı (Miktar Kıyaslaması):

Aynı ortamdaki nesne miktarlarının birbiriyle kıyaslanması için bölme işlemi yapılır.

Bu bölme işlemine miktar oranı veya bulunma oranı demekteyiz.

Örnek: Bir sınıfta 5 kız 7 erkek öğrenci varsa,

* Kızların sayısının, erkeklerin sayısına oranı 5/7’dir.

* Erkek sayısının, kızların sayısına oranı 7/5’dir.

Herhangi bir nesne miktarının, tüm miktara bölünerek elde edilen kıyaslamalar da yapılabilir. Genelde bu tür miktar kıyaslarında, tüm madde miktarıyla oranlandığından bahsedilmez. Bunu biz anlamalıyız.

Bu kıyaslamalarda elde edilen oran negatif ve 1’den büyük olamaz.

*Sınıftaki kız sayısının oranı 5/12’dir.

*Sınıftaki erkek sayısının oranı 7/12’dir.

* Sınıftaki kus oranı 0/12 = 0’dır.

* Sınıftaki öğrenci oranı 12/12 = 1’dir.

Örnek: Kız sayısının oranı 1/4 olan 20 kişilik A sınıfı ile kız sayısının oranı 3/5 olan 30 kişilik B sınıfındaki öğrencilerin hepsi bir araya getirilerek yeni bir sınıf oluşturuluyor. Yeni sınıftaki kız sayısının oranı kaçtır?

Çözüm: Yeni sınıftaki kız sayısının oranı sorulduğundan yeni sınıftaki kız sayısına ve yeni sınıftaki tüm öğrenci sayısına ihtiyacımız vardır.

Yeni sınıftaki tüm öğrenci sayısı 20 + 30 = 50’dir.

A sınıfından katılan kız sayısı 20.1/4 = 5,

B sınıfından katılan kız sayısı 30.3/5 = 18 olduğundan yeni sınıfta 5 + 18 = 23 tane kız vardır.

O halde yeni sınıfın kız sayısının oranı 23/50’dir.

Oranı yüzde olarak ifade edersek %(23/50).100 = %46 yani yeni sınıfın kız sayısının yüzdesi 46’dır deriz.

Örnek: Bir gezi grubundaki bayanların sayısı erkeklerin sayısının %60’ına eşittir. Bu grupta bulunan bayanların sayısı 30’dan fazla olduğuna göre erkeklerin sayısı en az kaçtır?

Çözüm: Grupta x tane erkek varsa 3x/5 bayan vardır. 3x/5 > 30 verildiğinden x > 50 olmalıdır.

Erkekleri ne kadar az tutarsak, bayanların sayısı da o kadar az olur. Bunun için x = 51 deriz.

Sıklara bakarız, A sıkkında olduğunu görünce şüpheleniriz.

Çünkü bayan sayısı tamsayı olmalıdır. Bayan sayısı 3x/5 olduğundan x’i 5’e tam bölünen en küçük sayı olarak almalıyız.

O halde x = 55 diyerek, bayanların en az 33 kişi olduğunu anlarız.

Burada bulunan Matematik Yüzde Problemleri Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]