Olasılık Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Olasılık online ders anlatımı yapan gözde hocaların Olasılık konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Olasılık video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik Olasılık konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Olasılık konusu ile ilgili yazılı anlatım ve genel Olasılık formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)Olasılık Konu Anlatımı Videolar
Matematik Olasılık Konu Anlatımı 2 Şenol Hoca
Matematik Olasılık Konu Anlatımı 2 TeknoFem
Matematik Olasılık Konu Anlatımı 2 (Bağımlı – Bağımsız Olay ve Ayrık Olaylar) Hocalara Geldik
Matematik Olasılık Konu Anlatımı 3 (Bağımlı / Bağımsız Olay ve Ayrık Olaylar 2) Hocalara Geldik
Matematik Olasılık Konu Anlatımı 4 (Koşullu Olasılık) Hocalara Geldik
Matematik Olasılık Konu Anlatımı 1 Tonguc Akademi
[t2]
Sitemizde Aşağıda yer alan Matematik Olasılık Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Olasılık canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.
Matematik Olasılık Konu Anlatımı Yazılı
A. OLASILIK TERİMLERİ
1. Deney
Bir madeni para atıldığında yazı mı ya da tura mı geleceğini, bir zar atıldığında sonucun ne olacağını, tespit etme işlemidir.
2. Sonuç
Bir deneyin her bir görüntüsüne (çıktısına) verilen isimdir. Her bir sonuç bir örnek nokta olarak da adlandırılır.
3. Örnek Uzay
Bir deneyin bütün sonuçlarını eleman kabul eden kümedir. Diğer bir ifadeyle örnek noktaların tamamını eleman kabul eden kümedir. (Örnek uzaya evrensel küme de denir.) Örnek uzay genellikle E ile gösterilir.
4. Olay
Bir örnek uzayın her bir alt kümesine verilen isimdir.
5. ımkansız Olay
E örnek uzayı için boş kümeye imkansız (olanaksız) olay denir.
6. Kesin Olay
E örnek uzayına kesin (mutlak) olay denir.
7. Ayrık Olaylar
A ve B, E örnek uzayına ait iki olay olsun.
A Ç B = Æ ise A ve B olaylarına ayrık olaylar denir.
B. OLASILIK FONKSİYON
E örnek uzayının tüm alt kümelerinin oluşturduğu küme K olsun.
P : K ® [0, 1]
şeklinde tanımlanan P fonksiyonuna olasılık fonksiyonu denir. A Î K ise P(A) reel sayısına A olayının olasılığı adı verilir.
P fonksiyonu aşağıdaki koşulları sağlar.
1. Her A Î K için, 0 £ P(A) £ 1 dir.
2. Evrensel kümenin meydana gelme olasılığı, P(E) = 1 dir.
3. ımkansız olayların meydana gelme olasılığı P(Æ) = 0 dır.
4. A Î K, B Î K ve A Ç B = Æ ise, P(A È B) = P(A) + P(B) dir.
Kural
| E örnek uzayında herhangi iki olay A ve B; A nın tümleyeni A‘ olsun. P olasılık fonksiyonu olmak üzere,1. A Ì B ise P(A) £ P(B) dir.2. P(A‘) = 1 – P(A) dır.3. P(A È B) = P(A) + P(B) – P(A Ç B) dir. |
C. Eş OLUMLU ÖRNEK UZAY
Sonlu bir E = {e1, e2, e3, … , en} örnek uzayı için,
P(e1) = P(e2) = P(e3) = … = P(en)
ise E örnek uzayına eş olumlu örnek uzay denir.
E, eş olumlu örnek uzayı ve A Î E ise A olayının olasılığı,

dır.
Kural
|
n, paranın atılma sayısını veya para sayısını göstermek üzere, bu deneyde örnek uzay 2nelemanlıdır. |
D. BAğIMSIZ OLAYLAR VE BAğIMLI OLAYLAR
A ve B aynı örnek uzayına ait olaylar olsun. Bu olaylardan birinin elde edilmesi diğerinin elde edilmesini etkilemiyorsa A ve B olaylarına bağımsız olaylar denir. Eğer iki olay bağımsız değilse, bu olaylara birbirlerine bağımlıdır denir.
Kural
| A ve B bağımsız olaylar olmak koşuluylaP(A) ¹ 0 ve P(B) ¹ 0 ise,A nın ve B nin gerçekleşme olasılığıP(A Ç B) = P(A) × P(B) dir.A nın veya B nin gerçekleşme olasılığıP(A È B) = P(A) + P(B) – P(A Ç B) dir. |
E. KOşULLU OLASILIK
A ile B, E örnek uzayında iki olay olsun. P(B) > 0 olmak üzere; B olayının gerçekleşmiş olması halinde A olayının olasılığına, A olayının B olayına bağlı koşullu olasılığı veya kısaca A nın B koşullu olasılığı denir ve P(A / B) şeklinde gösterilir.
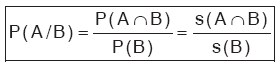
Burada bulunan Matematik Olasılık Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]







