İkinci Dereceden Eşitsizlikler Konu Anlatımı Video

b) Δ=0 ise; ax²+bx+c denkleminin x₁=x₂ çakışık iki kökü vardır.

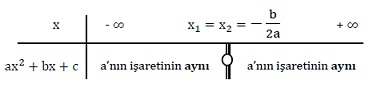
c) Δ<0 ise; ax²+bx+c denkleminin reel kökü yoktur.

Çarpım ve Bölüm Durumundaki Eşitsizlikler

f(x)= P(x).Q(x) / H(x) biçimindeki bir eşitsizliğin işareti incelenirken H(x)≠0 olmak üzere P(x), Q(x) ve H(x) polinomlarının kökleri ayrı ayrı bulunup tek bir tabloya yerleştirilir. Tabloda işareti belirlemek için yapılması gereken şöyledir:

• Önce bütün polinomların baş katsayılarının işaretine göre genel işaret belirlenir.
• Tablo oluşturulup daha önceden bulduğumuz bütün kökler küçükten büyüğe tabloya yerleştirilir.
• En son olarak tablonun sağından genel işaret ile işaretlemeye başlanır.
• Her kökte işaret değiştirilip sola doğru ilerlenir.
* Çift katlı köklerde ve mutlak değerin kökünde işaret değiştirmeden devam edilir.

Örnek:x²-3x+2>0 eşitsizliğinin çözüm kümesi=?
Önce x²-3x+2 denkleminin köklerini bulmak gerekir.
b²-4ac=(-3)²-4.1.2>0 olduğundan denklemin farklı iki kökü vardır
x1=3-1/2 ve x2=3+1/2 den x1=1 ve x2=2 bulunur.Buna göre işaret tablosu yapılarak kökler yerleştirilip , işaretler incelenerek çözüm kümesi yazılıyordur.
x,e 1 den küçük(x1<1) ya da 2 den büyük(x²>2) değerler verilirse x²-3x+2 ifadesi pozitif değer,x,e 1 ve 2 arasında(kökler arasında bir değer) verilirse x2-3x+2 ifadesi negatif bir değer alır buna göre;
Çözüm kümesi=Ç=(-sonsuz,1)U(2,+sonsuz) olur.

B)b²-4ac=0 ise denklemin tek kökü vardır(x=-b/2a) buna göre ax²+bx+c ifadesi a ile aynı işaretli olmuş olur
Örnek:-9x²+6x-1<0 eşitsizliğinin çözüm kümesi=?
b²-4ac=0 yani 36-4.(-9).(-1)=36-36=0 olduğunda denklemin kökü -b/2a dır buradan -6/2.(-9)=6/18=1/3 bulunur yani -9x²+6x-1 iafdesi x=1/3 noktasında sıfır değerini almaktadır diğer alanlarda negatif değerdedir (a ile aynı işaretli) Buna göre ;
Çözüm kümesi=Ç=IR-(1/3)=(-sonsuz,1/3)U(1/3,+sonsuz) olur.

C)b²-4ac<0 ise denklemin kökü yoktur.ax² +bx+c ifadesi a ile herzaman aynı işaretlidir tabloda .
Örnek:  x²–4x+5<0 eşitsizliğinin çözüm kümesi=?
b²-4ac<0=16-4.5=-4<0 olduğu için eşitsizlik a ile aynı işaretli olur a nın işareti pozitif olduğu için eşitsizlik tabloda daima pozitif değer alır Hiçbir noktada sıfır veya negatif olmaz .Bu nedenle eşitsizliğin Çözüm kümesi=O yani boş kümedir.