Egitim-Dünyası

Matris Determinant Konu Anlatımı Video

Matris Determinant Konu Anlatımı Video

LYS Sınavına hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan ve matematik 2 diye tabir edilen alanda yer alan matematik Matris Determinant online ders anlatımı yapan gözde hocaların Matris Determinant konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Matris Determinant video konu anlatımlarını listeledik, Değerli okuyucumuz LYS için olan ve mat 2 konuları arasında yer alan online matematik Matris Determinant konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Matris Determinant konusu ile ilgili yazılı anlatım ve genel Matris Determinant formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.) Matris Determinant Konu Anlatımı Videolar

Ekol HocaTeknoFem 1TeknoFem 2Halit Hoca 1Halit Hoca 2KörfezDetay HocaMatematik Matris Determinant Çözümlü Sorular ve FormüllerDiğer
Matematik Matris Konu Anlatımı Ekol Hoca

Matematik Determinant Konu Anlatımı Ekol Hoca

Matematik Matris (Matris Çeşitleri) Konu Anlatımı 1 TeknoFem

Matematik Matris (Matrislerde Toplama – Çıkarma – Çarpma) Konu Anlatımı 2 TeknoFem

Matematik Matris (Matrisin Özellikleri) Konu Anlatımı 3 TeknoFem

Matematik Matris (Matrisin Tersi) Konu Anlatımı 4 TeknoFem

Matematik Determinant (Tanım – Minör – Kofaktör) Konu Anlatımı 1

Matematik Determinant (Determinantın Özellikleri ) Konu Anlatımı 2

Matematik Determinant (Kare Matrisin Tersi) Konu Anlatımı 3

Matematik Matris Konu Anlatımı

Matematik Determinant Konu Anlatımı

Matematik Matris (matris nedir,matrisin tanımı) Konu Anlatımı 1

Matematik Matris (matris türleri ) Konu Anlatımı 2

Matematik Matris (matrislerde eşitlik,matrislerde toplama ve çıkarma) Konu Anlatımı 3

Matematik Matris (Bir matrisin bir skaler(reel) ile çarpılması,iki matrisin çarpılması,çarpma işleminin özellikleri) Konu Anlatımı 4

Matematik Determinant (Determinantın tanımı,1×1 ve 2×2 türündeki determinantlar) Konu Anlatımı 1

Matematik Determinant (Sarrus kuralı ile Determinant hesaplama (3×3 tipindeki matrisler)) Konu Anlatımı 2

Matematik Determinant (Minör,Kofaktör) Konu Anlatımı 3

Matematik Determinant (Bir matrisin transpozesi (devriği) , transpozun özellikleri ) Konu Anlatımı 4

Matematik Determinant (Bir kare matrisin tersinin hesaplanması ve ters matrisin özellikleri.) Konu Anlatımı 5

Matematik Determinant (Bir matrisin Ek matrisini hesaplama) Konu Anlatımı 6

Matematik Determinant (Determinanta ait özellikler ve bu özellikleri kullanarak daha hızlı determinant hesaplama.) Konu Anlatımı 7

Matematik Determinant (Lineer denklem sisteminin matris forma dönüştürülmesi,çözüm kümesinin Cramer kuralı ile bulunması,çözüm kümesinin boş küme , sonsuz elemanlı olma durumuları ) Konu Anlatımı 8

Matematik Matris Konu Anlatımı 1

Matematik Matris Konu Anlatımı 2

Matematik Matris Konu Anlatımı 3

Matematik Determinant Konu Anlatımı 4

Matematik Matris Determinant Konu Anlatımı 5

Matematik Matris Determinant Konu Anlatımı 6

Matematik Matris Konu Anlatımı

Matematik Determinant Konu Anlatımı

Matematik

Matris Determinant

SORU ÇÖZÜMLERİ VE FORMÜLLERi
[t1]
[t2]
Sitemizde Yukarıda yer alan Matematik Matris Determinant Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Matris Determinant canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.

Matematik Matris Determinant Konu Anlatımı Yazılı

A. MATRİSİN TANIMI

i, j, m, n sayma sayıları; i ≤ m, j ≤ n ve her i, j için aij reel sayılar olmak üzere,

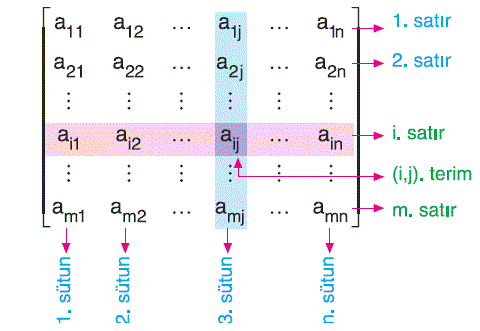
matris 1

şeklinde, bir cismin elemanlarının sıralı bir tablosuna m ´ n türünde (m tane satır ve n tane sütun) bir matris denir.

Matrisler büyük harfle gösterilir. Tablodaki yatay sıralara satır, düşey sıralara sütun adı verilir.

a13
a23
a33
…
ai3
…
am3  elemanları, A matrisinin 3. sütununu oluşturmaktadır.		 a11  a12  a13  …  a1j  …  a1n  elemanları, A matrisinin 1. satırını oluşturmaktadır.

Burada aij genel terimi gösterir. i, satır numarası ve j, sütun numarasıdır.

Bu matrisin m kadar satırı, n kadar sütunu vardır.

B. MATRİS ÇEŞİTLERİ

1. Sıfır Matrisi

Bütün elemanları sıfır olan matrise sıfır matrisi denir.

2. Kare Matrisi

Matris Determinant Konu Anlatımı www.egitim-dunyasi.net

Satır ve sütun sayısı eşit olan matrise kare matris denir. Kare matrislerde satır veya sütun sayısına matrisin mertebesi adı verilir.

A matrisi (4 ´ 4 boyutlu) 4 satırlı ve 4 sütunlu bir kare matristir.

A  kare matrisindeki a11  a22  a33 a44   terimlerinin oluşturduğu köşegene asal köşegen denir.

3. Birim Matris

Matris Determinant Konu Anlatımı www.egitim-dunyasi.net

Bütün köşegen elemanları 1 ve diğer bütün elemanları sıfır olan kare matrislere birim matris denir ve birim matris I harfi ile gösterilir. örnekteki matris 4 ´ 4 boyutlu birim matristir.

C. MATRİSLERİN EŞİTLİĞİ

Aynı türden iki matrisin, bütün aynı indisli terimleri eşit ise, bu matrisler eşittir. Bu ifadenin tersi de doğrudur. Yani, eşit iki matrisin, aynı indisli bütün terimleri eşittir.

D. MATRİSİN DEVRİĞİ (TRANSPOZU)

Bir matrisin devriği (transpozu) satırların sütun, sütunların satır haline getirilmesiyle elde edilen matristir.

Bir A matrisinin transpozu AT ya da Ad biçimlerinden biri ile gösterilebilir.

A=[aij]mxn  ise AT = [aji]nxm   olur.

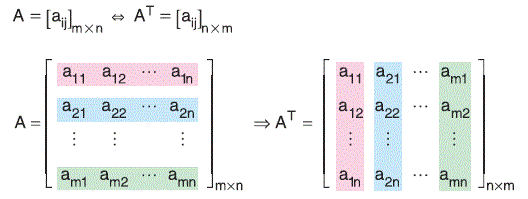
matris 3

E. MATRİSİN REEL SAYI İLE ÇARPIMI

Bir matrisi bir reel sayı ile çarpmak demek, matrisin bütün elemanlarını, o reel sayı ile çarpmak demektir. Yani; r bir reel sayı, A bir matris ve A’nın i’ninci satırının j’ninci sütunundaki eleman aijolmak üzere; r.A matrisinin i’ninci satırının j’ninci sütunundaki eleman r.aij‘dir. Bir matris c gibi bir sayı ile çarpılınca matrisin bütün elemanları c ile çarpılır.

A=[aij]mxn  ve c∈ R  ise  c.A = [c.aij]mxn  olur

F. MATRİSLERİN TOPLAMI

Sadece aynı türden olan matrisler toplanabilir. Matrisleri toplarken karşılıklı elemanlar toplanır. Yani; A ve B, m x n türünde iki matris, A’nın i’ninci satırının j’ninci sütunundaki eleman aij ve B’nin i’ninci satırının j’ninci sütunundaki eleman bij olmak üzere, A+B matrisinin i’ninci satırının j’ninci sütunundaki eleman aij+bij‘dir.

A=[aij]mxn

B= [bij]mxn ise 

A – B =[aij + bij]mxn  olur.

 

G. MATRİSLERİN FARKI

Aynı türden matrisler çıkarılır. Bunun için, aynı indisli terimler çıkarılır.

A=[aij]mxn

B= [bij]mxn ise 

A – B =[aij – bij]mxn  olur.

Özellik

  1.  A + B = B + A (Değişme özelliği vardır.)
  2.  A + (B + C) = (A + B) + C (Birleşme özelliği vardır.)
  3. A + O = O + A = A (Sıfır matrisi toplamaya göre birim (etkisiz) elemandır.)
  4.  A + (–A) = O (–A matrisi A matrisinin toplamaya göre tersidir.)
  5.  (A + B)T = AT + BT
  6.  (A – B)T = AT – BT
  7. k × (A + B) = k × A + k × B      (k∈R)
  8.  k × (A – B) = k × A – k × B     (k∈R)
  9. (k + p) × A = k × A + p × A     (k,p∈R)
  10. k × (p × A) = (k × p) × A     (k,p∈R)

H. İKİ MATRİSİN ÇARPIMI

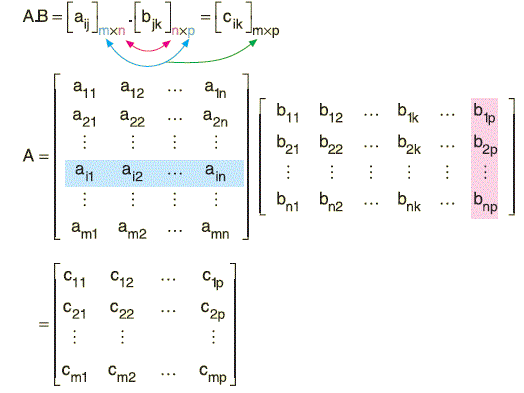
A ve B iki matris olmak üzere; A.B çarpım matrisi ancak ve ancak A matrisinin sütun sayısı Bmatrisinin satır sayısına eşit olduğunda vardır ve A.B matrisinin, satır sayısı, A’nın satır sayısına, sütun sayısı ise B’nin sütun sayısına eşittir.

m ´ n türünde A matrisi ile n ´ p türünde B matrisinin çarpımı m ´ p türünde olur.

Çarpma işlemi birinci matrisin satırları ile ikinci matrisin sütunları çarpılıp toplanarak yapılır.

matris 2

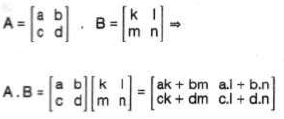
Matris Determinant formüller www.egitim-dunyasi.net

 

Özellik

  1.  A × B ¹ B × A (Değişme özelliği yoktur. Ancak bazı özel durumlarda eşitlik olabilir.) A × I = I × AAm × An = Am + nA–1× A = A × A–1
  2.  A × (B × C) = (A × B) × C (Birleşme özelliği vardır.)
  3.  A × (B + C) = A × B + A × C(B + C) × A = B × A + C × AÇarpma işleminin toplama işlemi üzerine sağdan ve soldan dağılma özelliği vardır.
  4.  A × B = O ise A = O veya B = O olması gerekmez.
  5.  A × I = I × A = A (I matrisi çarpmaya göre etkisiz elemandır.)
  6.  A × B = B ise A = I olması gerekmez.
  7.  (A × B)T = BT × AT
  8. (A × B × C)T = CT × BT × AT

I. KARE MATRİSİN KUVVETİ

A bir kare matrisi I birim matris ve m, n pozitif tam sayı olmak üzere, matrisin kuvveti aşağıdaki biçimde ifade edilir.

A0 = I
A1 = A
A2 = A.A
…
An = An-1.A

Ayrıca,

(Am)n = Am.n   olur.

Birim matrisin bütün kuvvetleri yine birim matristir. In = I

Kural

2 × 2 boyutundaki bazı özel matrislerin büyük kuvvetleri karşımıza çıkabilir.Bu özel durumların başlıcaları şunlardırMatris Determinant Konu Anlatımı www.egitim-dunyasi.net

Matris Determinant Konu Anlatımı www.egitim-dunyasi.net
Örnek:matris örnek1 Örnek:
matris örnek5
Örnek:
matris örnek3		 Örnek:
matris örnek2
Örnek:
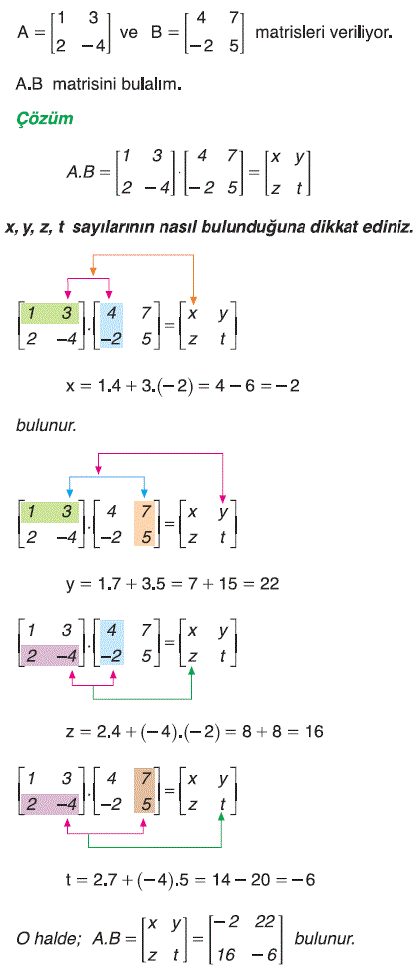matris örnek4		 Örnek:
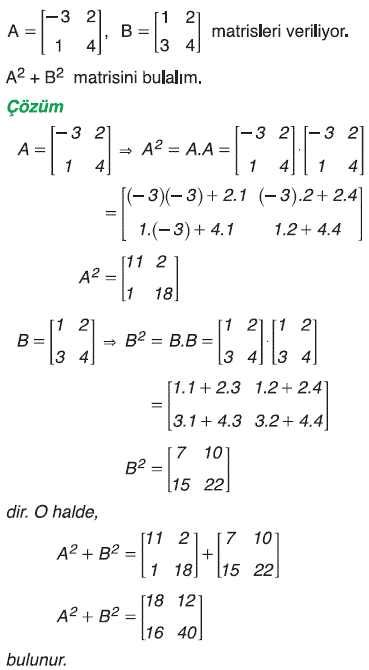matris örnek6

J. MATRİSİN DETERMİNANTI

Determinant, kare matrisleri bir sayıya eşleyen fonksiyondur. Determinant fonksiyonunun, kare matrisi eşlediği o sayıya matrisin determinantı denir.

A matrisinin determinantı, detA veya |A| biçiminde gösterilir. |A|, matrislerde mutlak değer anlamına gelmez. |A| sıfır veya negatif de olabilir.

Kural

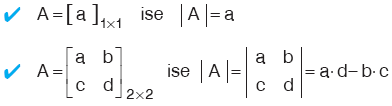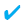 Matris Determinant Konu Anlatımı www.egitim-dunyasi.netMatris Determinant Konu Anlatımı www.egitim-dunyasi.netTürü ne olursa olsun, birim matrisin determinantı 1 dir.

Örnek:

matris örnek7

1.1 Sarrus Kuralı

A = [aij]3×3 biçimindeki matrislerin determinantını bulmak için Sarrus kuralı kullanılır.

Matris Determinant Konu Anlatımı www.egitim-dunyasi.net

3 ´ 3 türündeki bir matrisin determinantı şöyle bulunur:

1. İlk iki satır sırasıyla alta birer defa daha yazılır.

2. Köşegeni oluşturan a11, a22, a33 çarpılır; çarpım sağa yazılır.

3. Köşegenin hemen altındaki a21, a32, a13 çarpılır; çarpım sağa yazılır.

4. Aynı yaklaşımla a31, a12, a23 çarpılır; çarpım sağa yazılır.

5. Sağa yazılan üç çarpımın toplamı T1 olsun

6. Diğer köşegeni oluşturan a13, a22, a31 çarpılır; çarpım sola yazılır.

7. Diğer köşegenin hemen altındaki a23, a32, a11 çarpılır; çarpım sola yazılır.

8. Aynı yaklaşımla a33, a12, a21 çarpılır; çarpım sola yazılır.

9. Sola yazılan üç çarpımın toplamı T2 olsun,

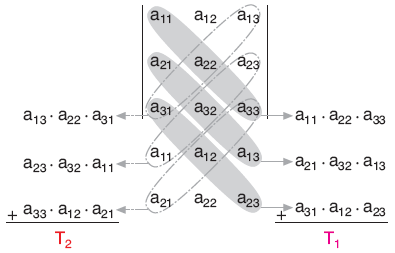
Matris Determinant Konu Anlatımı www.egitim-dunyasi.net

10. A matrisinin determinantı: detA = T1 – T2 dir.

2.Minör

A bir kare matris, A matrisinin i’ninci satırının j’ninci sütunundaki eleman aij olsun. A matrisinin herhangi bir aij elemanının ait olduğu satır ve sütundaki elemanların silinmesi sonucu elde edilenmatrisin determinantına, aij elemanının minörü denir ve Mij ile gösterilir.

3. İşaretli Minör (Kofaktör)

Bir kare matriste aij elemanının minörü Mij olsun.

aij elemanının işaretli minörü (kofaktörü):Aij = (-1)i+j.Mij

Kural

 A=[aij]mxn matrisi verilsin. Bir matrisin determinantı, bu matrisin herhangi bir satır veya sütun elemanları ile bu elemanların işaretli minörlerinin çarpımlarının toplamına eşittir.i. satıra göre determinant:|A| = ai1.|A| = ai1.Ai1 + ai2.Ai2 + … + ain.Ain + ai2.Ai2 + … + ain.Ainj. sütuna göre determinant: |A| = a1j.A1j + a2j.A2j + … + anj.Anj

4. Determinantın Özellikleri

Özellik

  •  Bir satır veya bir sütunun tüm elemanları sıfır olan matrislerin determinantı sıfırdır.
  •  Herhangi iki satır veya iki sütunun elemanları eşit olan matrisin determinantı sıfırdır.
  •  Herhangi iki satır veya iki sütunun elemanları orantılı olan matrisin determinantı sıfırdır.
  •  Herhangi iki satır veya iki sütunun yerleri değişirse determinantının işareti değişir.
  • Bir kare matrisin determinantı ile transpozunun determinantı eşittir.
  • Kare matrislerin çarpımlarının determinantı, bu matrislerin determinantları çarpımına eşittir.  det(A × B) = detA × detB
  • Bir kare matrisin kuvvetinin determinantı, determinantının kuvvetine eşittir.  detAn = (detA)n
  •  Bir kare matrisin çarpmaya göre tersinin determinantı, determinantının tersine eşittir.   |A| = 1/|A|  (|A| ≠ 0)
  • A = [aij]m×n matrisinin k ile çarpımının determinantı, A nın determinantının kn ile çarpımına eşittir. A=[aij]nxn ise |k.A| = kn.|A| olur
  • Bir kare matrisin bir satır ve bir sütunun tüm elemanları k ile çarpılırsa, elde edilen matrisin determinantı ilk matrisin determinantının k ile çarpımına eşittir.
  • Bir matrisin herhangi bir satırını k ile çarpıp diğer bir satıra ekleyince veya herhangi bir sütununu k ile çarpıp diğer bir sütuna ekleyince determinantının değeri değişmez.
  • Sadece bir satır veya bir sütun elemanları farklı olan matrislerin determinantları toplamı, diğer satır veya sütunları aynı olan ve farklı sütunu farklı sütunların toplamı kadar olan yeni matrisin determinantına eşittir.
Örnek:
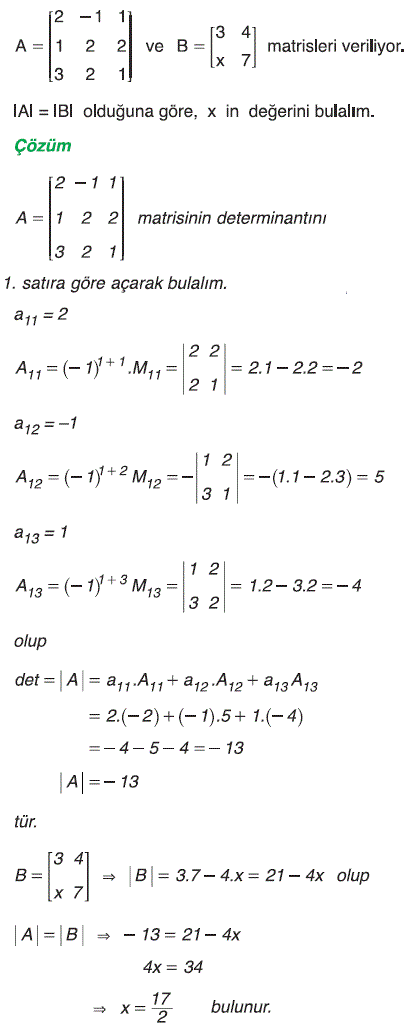matris örnek8		 Örnek:matris örnek9

K. EK MATRİS (ADJOİNT MATRİS)

Bir matrisin elemanları yerine, o elemanların işaretli minörlerinin yazılıp transpozu alınarak elde edilen matrise ek matris denir ve Ek(A) biçiminde gösterilir.

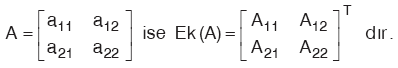
Matris Determinant Konu Anlatımı www.egitim-dunyasi.net

L. BİR MATRİSİN ÇARPMA İŞLEMİNE GÖRE TERSİ

A = [Aij]m×m biçimindeki kare matrislerin, çarpmaya göre tersini A–1 biçiminde gösteririz.

Determinantı sıfırdan farklı matrislerin tersi vardır.

|A| = (1/|A|).Ek(A)     (|A| ≠ 0)

Kural

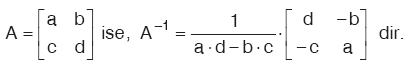Matris Determinant Konu Anlatımı www.egitim-dunyasi.net

Özellik

  1. A-1.A =A.A-1 = ı
  2. (A-1)-1 = A
  3. (A-1)T = (AT)-1 
  4. (k.A)-1 = (1/k).A-1    (K∈R)
  5. (A.B)-1 = B-1.A-1

Burada bulunan Matematik Matris Determinant Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]

ZİYARETÇİ YORUMLARI

Henüz yorum yapılmamış. İlk yorumu aşağıdaki form aracılığıyla siz yapabilirsiniz.

BİR YORUM YAZ