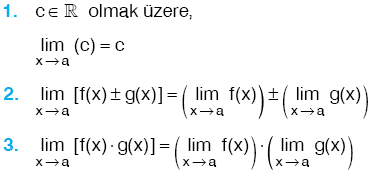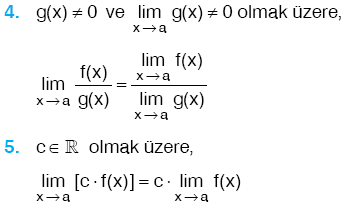Limit ve Süreklilik Konu Anlatımı Yazılı

Öncelikle Bu derse nasıl çalışmanız gerektiği ile ilgili bir kaç küçük öneride bulunursak;
Limit ve Süreklilik konusuda diğer LYS matematik konuları gibi öğrencilerin gözünde korkulan bir konudur ama düzenli çalışma tekrar ve pratik yollar ile konu hem rahat bir şekilde öğrenilebilir hem de öğrenme aşaması zevkli bir hal alarak sıkıcılıktan kendimizi kurtarabiliriz. Limit ve Süreklilik konusuna çalışmaya başlamadan önce ilk olarak bu konuyla alakalı kafamızda oluşturduğumuz ön yargıları kaldırıp bu derse olumlu bir şekilde bakarak “Ben bu dersi rahatlıkla öğrenebilirim ve yapabilirim” diyerek başlayın.
Limit ve Süreklilik konu anlatımı olarak bakıldığında diğer kısa anlatımı olan matematik konuları içinde yer almıyor ama birçok konu da yer alan kafa çeldirici soruların bu konu içinde çok fazla bulunmaması ise sizin avantajınız haline gelebilir. Çünkü düz mantık formülü yerine koy çözümü al sistemi bu konu içinde daha etkidir. Eğitim-Dünyası olarak bu konuyu biraz uzun olması hasebiyle 3 e bölmüş bulunmaktayız. ilk olarak burada yazımızın devamında yer alan yazılı konu anlatımı bulunuyor 2. olarak ise Türkiye’nin internette en çok tercih edildiğini düşündüğümüz 8 tane farklı hocasının videolu konu anlatımlarının bulunduğu konumuz (Limit ve Süreklilik Konu Anlatımı Video) yer almaktadır, ardından ve 3. olarak ise konu dersini tamamen çalıştıktan sonra konuyu iyice pekiştirmenizi sağlayacak olan yine farklı hocaların anlatımıyla çözümlü sorular yer almaktadır ve bu çözümlü soruların içinde LYS de çıkmış sorularda çözümleriyle birlikte video olarak bulunmaktadır. Tabi buraya bir de Limit ve Süreklilik formüllerini eklemiş bulunmaktayız .(Limit ve Süreklilik Çözümlü Sorular ve Formüller)
Şimdi bu kadar anlatımın ve çözümlü sorunun yer aldığı dökümanları sağladıktan sonra basit bir şekilde nasıl etkili kullanabileceğiniz ile alakalı kendi yöntemimizi de aktaralım öncelikle yazılı anlatımda verdiğimiz konuyu şöyle bir göz ucuyla okuyun ardından video konu anlatımları sayfamıza geçerek istediğiniz hocadan (Burada bir hoca tavsiye etmiyoruz çünkü herkesin sevdiği tarz faklıdır, zaten sitemizden diğer derslere çalıştıysanız sabit takip etmek istediğiniz bir hoca mutlaka olacaktır) konu anlatımını biraz aralar vererek ve notlar alarak dinleyin verdiğiniz aralarda derse devam etmeden önce aldığınız notları bir kere okuyun ondan sonra derse devam edin, eğer dinlediğiniz hocadan çok bir şey anlamadığınızı düşünüyorsanız diğer hocaların anlatımlarını dinleyerek, hem bir nevi tekrar hem de farklı bir bakış açısı kazanarak konuyu daha iyi özümseyebilirsiniz ve konu anlatımını bitirdikten sonra varsa elinizdeki test kitaplarından bir test çözmeye çalışın, buradaki amaç bir nevi ilk başta kendinizi denemek, kesinlikle çok çözemediğiniz soru olursa kendinizi kötü hissetmeyin söylediğim gibi daha dersi bitirmedik sadece kendimizi denedik burada iyi kötü kendimiz ve takıldığımız noktaları görmüş olduk ve sırada 3. olarak bahsettiğimiz çıkmış ve normal soruların çözümleriyle beraber yer aldığı sayfamıza giderek buradaki hocalarımızın soru çözümlerini izleyiniz. Böylelikle hem çözdüğünüz testteki eksikliklerinizi giderebilirsiniz hem de çeşitli hocaların farklı sorulardaki çözümlerini izlediğiniz için sorular hakkında daha detaylı bakış açıları kazanarak konuyu çok iyi kavramış olursunuz. Burada aşağıya da ekleyeceğimiz bazı pratik yöntemlere de bakarak ve daha çok test çözerek hem konuyu hem de formülleri çok çaba sarf etmeden mantığıyla birlikte öğrenmiş olacaksınız. Dilimiz sürçtüyse affola, egitim-dunyasi.net olarak başarılar dileriz
Limit nedir ?
Limit kavramı ve tanımı, kavram olarak eski olmasına kaşın, tanımlanması ve kullanılması çok eski değildir. Örneğin limit ünlü ε−δ tekniği ile tanımlanması ve kullanılması ülü Alman Matematikçisi Eduard Heine (1821-1881) tarafından olmştur. Limit fizik ve mühendislikte yaygın olarak kullanılılır. Limit kavramının öğrencilere verilmesi, tanıtılması, öğretilmesi ve öğrenilmesi öyle o kadar da kolay değildir. Bunun için, limitin tanıtılmasına önce sezgisel olarak yaklaşalım. Daha sonra tam tanımını verelim.
f(x) fonksiyonu verilsin. x noktası bir a noktasına yeteri kadar yaklaşsın. x noktasının a noktasına reel eksen üzerinde sağdan ve soldan olmak üzere, iki yönlü yaklaşımı vardır.
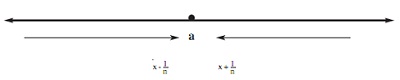
Burada, x değerinin a değerine eşit olması gerekmez. Bir çok durumda, a noktası, f(x) fonksiyonunun tanım bölgesinde olmayabilir. Yani, x noktası a noktasına (x≠a) sağdan ve soldan yaklaşırken f(x) fonksiyonu bir L sayısına yaklaşıyorsa f(x) fonksiyonunun bu a noktasında limiti vardır denir ve kısaca limit
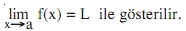
LİMİT
A. SOLDAN YAKLAŞMA, SAĞDAN YAKLAŞMA
x değişkeni a ya, a dan küçük değerlerle yaklaşıyorsa, bu tür yaklaşmaya soldan yaklaşma denir ve 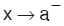 biçiminde gösterilir.
biçiminde gösterilir.
x değişkeni a ya, a dan büyük değerlerle yaklaşıyorsa, bu tür yaklaşmaya sağdan yaklaşma denir ve 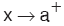 biçiminde gösterilir.
biçiminde gösterilir.
B. LİMİT KAVRAMI
Limit kavramını bir fonksiyonun grafiği üzerinde açıklayalım:
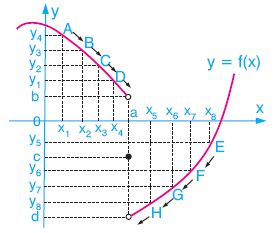
Grafiği verilen y = f(x) fonksiyonu için, apsisleri; x = a nın solunda yer alan ve giderek a ya yaklaşan A(x1, y4) , B(x2, y3) , C(x3, y2) , D(x4, y1), … noktalarını göz önüne alalım:
Bu noktaların apsisleri olan x1, x2, x3, x4, … giderek a ya yaklaşırken, ordinatları
f(x1) = y4, f(x2) = y3, f(x3) = y2, f(x4) = y1, … giderek b ye yaklaşır.
Bu durumu; x, a ya soldan yaklaşıyorken f(x) b ye yaklaşır şeklinde ifade edebiliriz. Bu durumda,
f(x) in x = a daki soldan limiti b dir denir. Ve
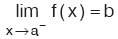
şeklinde gösterilir.
Yukarıdakine benzer şekilde, apsisleri x = a nın sağında yer alan ve giderek a ya yaklaşan
E(x8, y5) , F(x7, y6) , G(x6, y7) , H(x5, y8) , … noktalarını göz önüne alalım.
Bu noktaların apsisleri olan x8, x7 , x6 , x5 , … giderek a ya yaklaşırken, ordinatlar f(x8) = y5 , f(x7) = y6 , f(x6) = y7 , f(x5) = y8 , … giderek d ye yaklaşır.
Bu durumu “x, a ya sağdan yaklaşıyorken f(x) d ye yaklaşır.” şeklinde ifade edebiliriz.
Bu durumda; f(x) in x = a daki sağdan limiti d dir denir. Ve
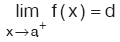
biçiminde gösterilir.
Kural
f(x) fonksiyonunun x = a daki soldan limiti sağdan limitine eşit ise fonksiyonun x = a da limiti vardır ve x in a noktasındaki limiti L ise, 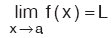 biçiminde gösterilir. x = a daki sağ limit ve sol limit değeri, fonksiyonun x = a daki limitidir.f(x) fonksiyonunun x = a daki soldan limiti sağdan limitine eşit değil ise fonksiyonun x = a da limiti yoktur. biçiminde gösterilir. x = a daki sağ limit ve sol limit değeri, fonksiyonun x = a daki limitidir.f(x) fonksiyonunun x = a daki soldan limiti sağdan limitine eşit değil ise fonksiyonun x = a da limiti yoktur. |
C. UÇ NOKTALARDAKİ LİMİT
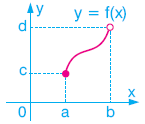
f fonksiyonu [a, b) aralığından [c, d) aralığına tanımlı olduğu için, uç noktalardaki limitleri araştırılırken, sadece tanımlı olduğu tarafın limitine bakılarak sonuca gidilir.
Fonksiyonun bir noktada limitinin olması için, o noktada tanımlı olması zorunlu değildir. Buna göre,
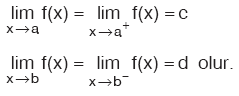
Kural
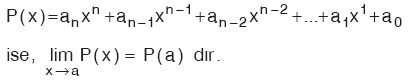 |
D. LİMİTLE İLGİLİ ÖZELLİKLER
Özellik
| f ve g , x = a da limitleri olan iki fonksiyon olsun
|
Özellik
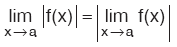 |
Özellik
 |
Özellik
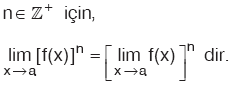 |
Özellik
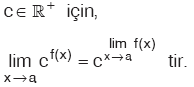 |
Özellik
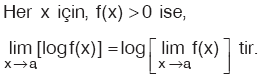 |
E. PARÇALI FONKSİYONUN LİMİTİ
Özellik
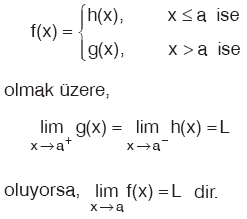 |
F. İŞARET FONKSİYONUNUN LİMİTİ
Özellik
f(x) = sgn [g(x)] olsun. Bu sonuç genellikle doğrudur. Fakat az da olsa bu sonuca uymayan örnekler vardır.Söz gelimi, f(x) = sgn(x2) fonksiyonunun x = 0 da limiti vardır ve 1 dir. |
G. TAM DEĞER FONKSİYONUNUN LİMİTİ
Özellik
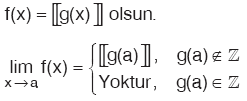 Bu sonuç genellikle doğrudur. Fakat az da olsa bu sonuca uymayan örnekler vardır.Söz gelimi, Bu sonuç genellikle doğrudur. Fakat az da olsa bu sonuca uymayan örnekler vardır.Söz gelimi, 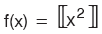 fonksiyonunun x = 0 da limiti vardır. fonksiyonunun x = 0 da limiti vardır.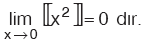 |
H. 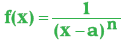 NİN x = a DAKİ LİMİTİ
NİN x = a DAKİ LİMİTİ
Özellik
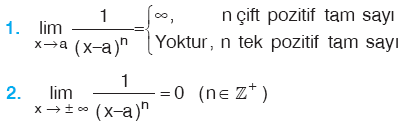 |
I. TRİGONOMETRİK FONKSİYONLARIN LİMİTİ
1. sinx in ve cosx in limiti
sinx ve cosx fonksiyonu bütün x reel değerleri için tanımlı olduğu için,
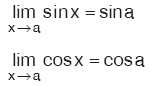
olur.
2. tanx in limiti
tanx fonksiyonu 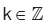 olmak üzere,
olmak üzere,
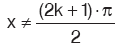 koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,
koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,
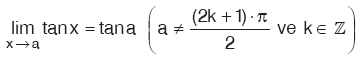
olur.
Sonuç
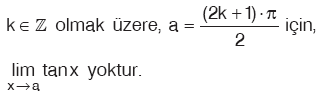 |
3. cotx in limiti
cotx fonksiyonu 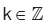 olmak üzere,
olmak üzere, 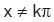 koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,
koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,
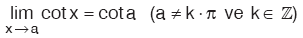
olur.
Sonuç
 |
J. BELİRSİZLİK DURUMLARI
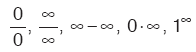
belirsizlikleriyle karşılaştığımızda aşağıda verilen yöntemler kullanılarak limit hesaplanır. Bu limitler türevin içinde vereceğimiz L’Hospital kuralıyla da hesaplanabilir.
Kural
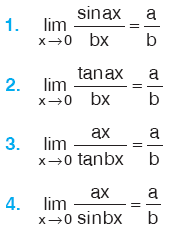 |
Kural
m, n Î N olmak üzere, 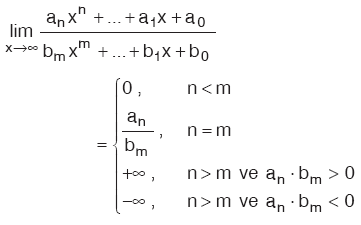 olur. olur. |
Kural
a > 0 olmak üzere, ¥ – ¥ belirsizliği olan limitler, 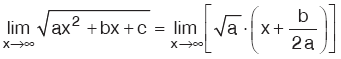 kuralını kullanarak hesaplanabilir. kuralını kullanarak hesaplanabilir. |
Kural
 Buna göre, 0 × ¥ belirsizliği Buna göre, 0 × ¥ belirsizliği 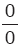 veya veya 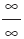 belirsizliğine dönüştürülerek sonuca gidilir. belirsizliğine dönüştürülerek sonuca gidilir. |
Kural
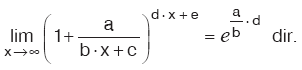 |
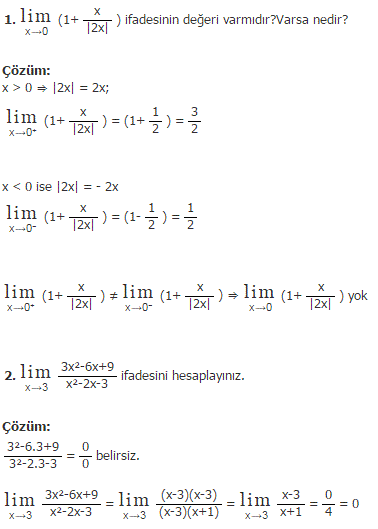 …………………………………………………………………………………………. …………………………………………………………………………………………. | 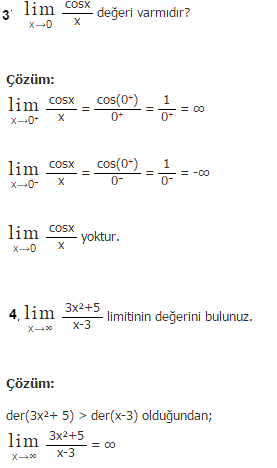 …………………………………………………………………………. …………………………………………………………………………. |
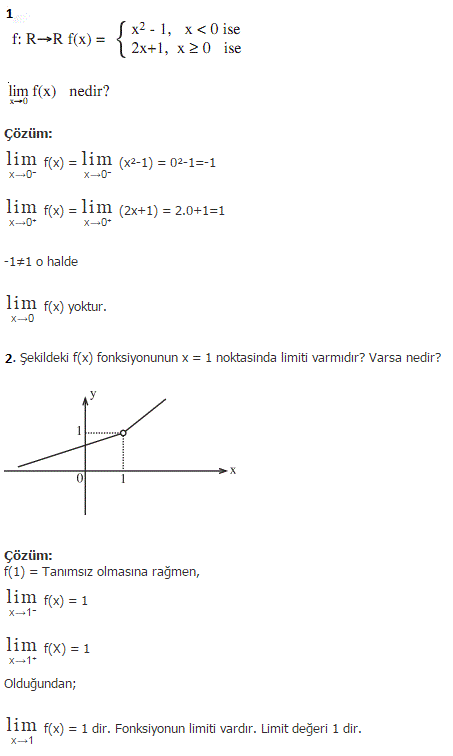 | 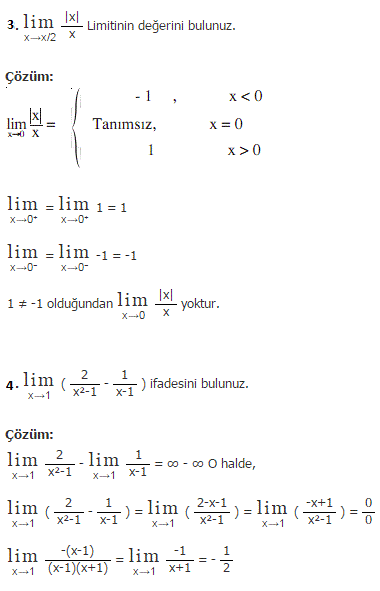 |
II. SÜREKLİLİK
Süreklilik nedir?
Limit kavramı ile süreklilik kavramının birbiriyle çok yakın ilşkisi vardır. Kısaca söylemek gerekirse, süreklilik bir limit problemidir.
A ⊂ IR olmak üzere f: A → IR fonksiyonu verilsin ve a ∈ A olsun. Eğer Lim f(x) ( x → a ) limiti varsa ve bu limit f(x) fonksiyonunun x = a noktasındaki değeri olan f(a) ya eşitse,ise y = f(x) fonksiyonu x = a noktasında sürekli dir denir.
Kural
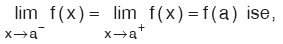 f(x) fonksiyonu apsisi x = a olan noktada süreklidir. f(x) fonksiyonu apsisi x = a olan noktada süreklidir. |
Sonuç
y = f(x) fonksiyonu x = a da sürekli ise,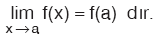 |
Uyarı
| f(x) fonksiyonu apsisi x = a olan noktada sürekli değil ise, süreksizdir. |
Kural
| 1. Bir fonksiyon bir noktada tanımsız ise, o noktada süreksizdir.2. Bir fonksiyon bir noktada limitsiz ise, o noktada süreksizdir.3. Bir fonksiyon bir noktada tanımlı ve limitli ancak, tanım değeri limit değerinden farklı ise, bu noktada süreksizdir. |
SAĞDAN SÜREKLİLİK
a bir reel sayı; I, a’yı eleman kabul eden bir açık aralık; f ise I’da tanımlı olan reel değerli bir fonksiyon olsun.
![]()
ise f fonksiyonu a noktasında sağdan süreklidir.
SOLDAN SÜREKLİLİK
a bir reel sayı; I, a’yı eleman kabul eden bir açık aralık; f ise I’da tanımlı olan reel değerli bir fonksiyon olsun.
![]()
ise f fonksiyonu a noktasında soldan süreklidir.
L’HOSPİTAL KURALI
A. L’HOSPİTAL KURALI
Bir fonksiyonun x = a noktasındaki limiti hesaplanırken karşımıza çıkan,
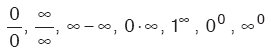
belirsizlikleri, 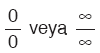 belirsizliklerinden birine dönüştürülerek,
belirsizliklerinden birine dönüştürülerek,
L’ Hospital Kuralı yardımıyla sonuçlandırılır.
Kural
f ve g, (a, b) aralığında türevlenebilir olsun. Her x Î (a, b) için g’(x) ¹ 0 ve c Î (a, b) olmak üzere,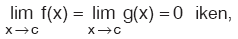 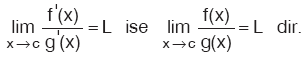 Eğer, Eğer, 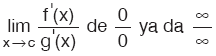 ise yukarıdaki kural birdaha uygulanır. ise yukarıdaki kural birdaha uygulanır. |
Uyarı
L’ Hospital kuralında 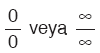 belirsizliğini ortadan kaldırmak için, yapılan işlemin: Payın türevini paya, paydanın türevini paydaya yazmak olduğuna dikkat ediniz. belirsizliğini ortadan kaldırmak için, yapılan işlemin: Payın türevini paya, paydanın türevini paydaya yazmak olduğuna dikkat ediniz. |
Kural
Sonusz × 0 belirsizliğinde,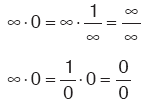 düzenlemelerinden biriyle sonuca gidilir. ¥– ¥ belirsizliğinde, 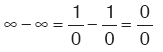 düzenlemesiyle sonuca gidilir. 00, ¥ , 1¥ belirsizliklerinde, 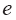 tabanında logaritma alınarak sonuca gidilir. tabanında logaritma alınarak sonuca gidilir. |
Konu ile Alakalı Çözümlü Örnekler
 |
 |
 |
 |
 |
- Matematik Limit ve Süreklilik Konu Anlatımlarını izlemek İçin Tıklayınız
- Matematik Limit ve Süreklilik Çözümlü soruları izlemek ve Limit ve Süreklilik İle İlgili Önemli Formüllere Ulaşmak İçin Tıklayınız
- LYS Matematik konu Anlatımları ve Çözümlü Sorular (MAT 2) için Tıklayınız
- Tüm LYS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm YGS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
Burada bulunan Matematik Limit ve Süreklilik Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]