Karmaşık Sayılar Konu Anlatımı Video

LYS Sınavına hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan ve matematik 2 diye tabir edilen alanda yer alan matematik Karmaşık Sayılar online ders anlatımı yapan gözde hocaların Karmaşık Sayılar konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Karmaşık Sayılar video konu anlatımlarını listeledik, Değerli okuyucumuz LYS için olan ve mat 2 konuları arasında yer alan online matematik Karmaşık Sayılar konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Karmaşık Sayılar konusu ile ilgili yazılı anlatım ve genel Karmaşık Sayılar formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.) Karmaşık Sayılar Konu Anlatımı Videolar
Matematik Karmaşık Sayılar Konu Anlatımı 2 Ekol Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 2 (Karmaşık sayılarda işlemler)Şenol Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 3 (karmaşık sayının mutlak değeri)Şenol Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 4 (Karamaşık sayılar arasındaki uzaklık) Şenol Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 5 (KARMAŞIK SAYILARIN KUTUPSAL GÖSTERİMİ) Şenol Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 6 (KARMAŞIK SAYIYI DÖNDÜRME,KARMAŞIK SAYIDA KÖK BULMA) Şenol Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 2 (KARMAŞIK SAYININ EŞLENİĞİ,KARMAŞIK SAYININ MUTLAR DEĞERİ (MODÜLÜ),KARMAŞIK SAYILARDA II. DERECEDEN DENKLEMİN ÇÖZÜMÜ,) TeknoFem
Matematik Karmaşık Sayılar Konu Anlatımı 3 (EŞLENİK VE MUTLAK DEĞER ÖZELLİKLERİ,İKİ KARMAŞIK SAYI ARASINDAKİ UZAKLIK,KARMAŞIK SAYININ GEOMETRİK YER DENKLEMİ VE DÜZLEMDEKİ GÖRÜNTÜSÜ,KARMAŞIK SAYILARDA İŞLEMLER) TeknoFem
Matematik Karmaşık Sayılar Konu Anlatımı 4 (DÜZLEMDE KARMAŞIK SAYI İLE ÇEMBERİN İLİŞKİSİ,KARMAŞIK SAYININ KUTUPSAL BİÇİMİ) TeknoFem
Matematik Karmaşık Sayılar Konu Anlatımı 5 (KARMAŞIK SAYININ KÖKLERİ) TeknoFem
Matematik Karmaşık Sayılar Konu Anlatımı 6 (KUTUPSAL BİÇİM ÖZELLİKLER,KARMAŞIK SAYININ DÖNDÜRÜLMESİ) TeknoFem
Matematik Karmaşık Sayılar Konu Anlatımı 2 (Bir karmaşık sayının eşleniği,karmaşık sayılarda toplama,çıkarma,bölme ve çarpma.) Halit Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 3 (Bir karmaşık sayının modülü( mutlak değeri) ve özellikleri… ) Halit Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 4 (İki karmaşık sayı arasındaki uzaklık ve karmaşık düzlemde gösterimi.) Halit Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 5 (Karmaşık Sayıların Kutupsal gösterimi.) Halit Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 6 (Karmaşık Sayıların Kutupsal gösterimi.) Halit Hoca
Matematik Karmaşık Sayılar Konu Anlatımı 7 (Bir Karmaşık sayının köklerinin bulunması,bir karmaşık sayının kompleks düzlemde döndürülmesi..) Halit Hoca
Matematik Karmaşık Sayılar Konu Anlatımı Yazılı
ax² + bx + c = 0 denkleminin Δ < 0 iken reel kökünün olmadığını daha önceden biliyoruz. Örneğin, x² + 1 = 0 denkleminin reel kökü yoktur. Çünkü,( x² + 1 = 0 Þ x² = -1 ) karesi –1 olan reel sayı yoktur.
Şimdi, bu türden denklemlerin çözümünü mümkün kılan ve reel sayılar kümesini de kapsayan yeni bir küme tanımlayacağız…
TANIM:
a ve b birer reel sayı ve i = √-1 olmak üzere, z = a + bi şeklinde ifade edilen z sayına Karmaşık ( Kompleks ) Sayı denir. Karmaşık sayılar kümesi C ile gösterilir.
C = { z : z = a + bi ; a, b Î R ve √-1 = i } dir.
( i = √-1 Þ i² = -1 dir.)
z = a + bi karmaşık sayısında a ya karmaşık sayının reel ( gerçel ) kısmı, b ye karmaşık sayını imajiner (sanal) kısmı denir ve Re(z) = a, İm(z) = b şeklinde gösterilir.
Örnek:
Z1 = 3 + 4i, Z2 = 2 – 3i, Z3 = √-1 + i, Z4 = 7, Z5 = 10i sayıları birer karmaşık sayıdır.
Z1 karmaşık sayısının reel kısmı 3, imajiner kısmı 4 tür.
Z2 = 2 – 3i Þ Re(Z2) = 2 ve İm(Z2) = -3,
Z3 = √-1 + i Þ Re(Z3) = √-1 ve İm(Z3) = 1,
Z4 = 7 Þ Re(Z4) = 7 ve İm(Z4) = 0,
Z5 = 10i Þ Re(Z5) = 0 ve İm(Z5) = 10 dur.
I. KARMAŞIK SAYILAR KÜMESİ
Tanım
Uyarı
a, b pozitif gerçel sayı vex, y negatif gerçel sayı olmak üzere,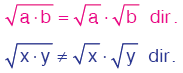 |
A. i NİN KUVVETLERİ
![]() olmak üzere,
olmak üzere,
i0 = 1 dir.
i1 = i dir.
i2 = –1 dir.
i3 = i2 × i1 = (–1) × i = –i dir.
i4 = i2 × i2 = (–1) × (–1) = 1 dir.
i5 = i4 × i1 = 1 × i = i dir.
Görüldüğü gibi i nin kuvvetleri ; 1, i, –1, –i değerlerinden birine eşit olmaktadır.
Sonuç
| Sanal sayı biriminin (i nin) kuvveti x olsun. x tam sayısı 4 ile bölündüğünde, kalan 0 ise, ix ifadesinin eşiti 1,kalan 1 ise,ix ifadesinin eşiti i,kalan 2 ise, ix ifadesinin eşiti –1,kalan 3 ise, ix ifadesinin eşiti –i dir.Buna göre, n tam sayı olmak üzere,i4n= 1,i4n+1 = i,
i4n+2 = –1, i4n+3 = –i dir. |
Tanım
| a ve b birer reel (gerçel) sayı ve |
Uyarı
| Her reel (gerçel) sayı imajiner kısmı 0 (sıfır) olan bir karmaşık sayıdır. Buna göre, karmaşık sayılar kümesi reel sayılar kümesini kapsar. Yani, |
B. İKİ KARMAŞIK SAYININ EŞİTLİĞİ
Reel kısımları ve imajiner kısımları kendi aralarında eşit olan iki karmaşık sayı birbirine eşittir.
Kural
| Z1=a+bi ve Z2=c+diZ1=Z2 ise, (a=c ve b=d) dir |
C. KARMAŞIK SAYILARIN ANALİTİK DÜZLEMDE BELİRTİLMESİ
Reel kısmı a, imajiner kısmı b olan karmaşık sayının; z = a + ib şeklindeki gösterimine karmaşık sayının standart (cebirsel) biçimi,
Z(a, b) biçimindeki gösterimine kartezyen koordinatlarıyla gösterilmiş biçimi denir.
Ox eksenine reel eksen, Oy eksenine de sanal (imajiner) eksen diyerek karmaşık sayıları gösterebileceğimiz karmaşık düzlemi elde ederiz.
Karmaşık sayılarla karmaşık düzlemin noktaları bire bir eşlenebilir.
z = a + bi karmaşık sayısının düzlemdeki görüntüsü (a, b) noktasıdır.
D. KARMAŞIK SAYININ EŞLENİĞİ
![]() ve i2 = –1 olmak üzere,
ve i2 = –1 olmak üzere,
a + bi ve a + (–b)i karmaşık sayılarından birine diğerinin eşleniği denir.
z karmaşık sayısının eşleniği![]() ile gösterilir.
ile gösterilir.
Buna göre,![]()
Kural
Bir karmaşık sayının eşleniğinin eşleniği kendisidir. Buna göre,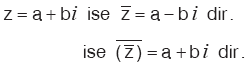 |
Kural
| Reel kat sayılı, ax2 + bx + c = 0 ikinci dereceden denkleminin köklerinden biri m + ni karmaşık sayısı ise diğeri m – ni sayısıdır. |
Örnek:
1) Z1 = 4 + 3i sayısının eşleniği Z1 = 4 – 3i,
2) Z2 = √2 – √3i sayısının eşleniği Z2 = √2 + √3i,
3) Z3 = -7i sayısının eşleniği Z3 = 7i,
4) Z4 = 12 sayısının eşleniği Z4 = 12,
5) Z5 = √3 – √2 sayısının eşleniği Z5 = √3 – √2 dir.
Örnek: Z = a + bi olmak üzere, 3 . Z – 1 = 2(4 – i) olduğuna göre, a + b toplamını bulalım.
Çözüm: 3 . Z – 1 = 2(4 – i)
3 . (a – bi) – 1 = 8 – 2i
3a – 1 – 3bi = 8 – 2i
olduğundan, 3a –1 = 8 ve -3b = -2 dir.
3a – 1 = 8 => 3a = 9 => a = 3 ve
-3b = -2 => b = 2/3 tür.
O halde, a + b = 3 + 2/3 = 11/3
Not:
- Bir karmaşık sayının eşleniğinin eşleniği kendisine eşittir ( (ž) = z )
- Reel katsayılı ikinci dereceden ax2 + bx + c = 0 denkleminin köklerinden biri Z = m + ni karmaşık sayısı ise diğeri bu kökün eşleniği olan Z = m – ni sayısıdır.
E. KARMAŞIK SAYILARIN MUTLAK DEĞERİ (MODÜLÜ)
Karmaşık düzlemde, bir karmaşık sayıya karşılık gelen noktanın başlangıç noktasına (orijine) olan uzaklığına bu sayının mutlak değeri veya modülü denir.
z karmaşık sayısının mutlak değeri |z| ile gösterilir.
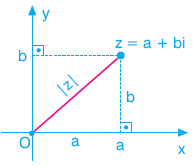 |
Yandaki dik üçgende Pisagor teoreminden de,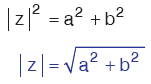 dir. dir. |
F. KARMAŞIK SAYILARDA İŞLEMLER
1. Toplama İşlemi
Karmaşık sayılar toplanırken, reel kısımlar kendi aralarında ve sanal kısımlar kendi aralarında toplanır. Buna göre,
i2 = –1 olmak üzere,
z=a+ib
w=c+id
karmaşık sayıları verilmiş olsun. Bu durumda,
z+w=(a+ib)+(c+id)
=(a+c)+i(b+d) dir
2. Çıkarma İşlemi
z + (–w) = z – w
olduğuna göre, z sayısını w sayısının toplama işlemine göre tersi ile toplamak, z sayısından w sayısını çıkarmak demektir. Buna göre,
z ile w nin farkı, reel kısımların birbiri ile sanal kısımların birbiri ile farkına eşittir. Reel kısımların farkı, sonucun reel kısmını; sanal kısımların farkı, sonucun sanal kısmını verir. Buna göre,
i2 = –1 olmak üzere,
z=a+ib
w=c+id
karmaşık sayıları verilmiş olsun. Bu durumda
z-w=(a+ib)-(c+id)
=(a-c)+i(b-d) dir
3. Çarpma İşlemi
Karmaşık sayılarda çarpma işlemi, i2 = –1 olduğu göz önüne alınarak, reel sayılardakine benzer şekilde yapılır.
z = a + bi ve w = c + di olsun. Buna göre,
z.w=a.c+a.di+b.ci+b.di2 , (i2=-1)
a.c+a.di+b.ci-b.d
(a.c-b.d)+(a.d+b.c)i
Sonuç
i2 = –1 ve z = a + bi olmak üzere,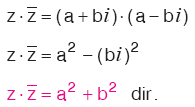 |
Kural
| i2 = –1 ve n tam sayı olmak üzere,(1+i)2.n = 2n.in dir(1-i)2.n = (-2n ).in dir |
4. Bölme İşlemi
![]()
z1 × (z2)–1 sayısına z1 in z2 ye bölümü denir ve Z1/Z2 biçiminde gösterilir.
Karmaşık sayılarda bölme işlemi, pay ile paydanın, paydanın eşleniği ile genişletilmesiyle yapılır. Yani,
z1 = a + bi ve z2 = c + di ise,
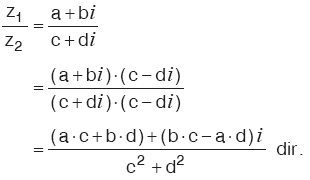
5. Eşlenik ve Mutlak Değerle İlgili Bazı Özellikler
z1 ve z2 birer karmaşık sayı olmak üzere,
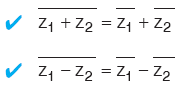

G. KARMAŞIK DÜZLEMDE İKİ NOKTA ARASINDAKİ UZAKLIK
z = a + bi ve w = c + di olsun.
|z – w|
ifadesinin değeri z ile w sayısı arasındaki uzaklığa eşittir.
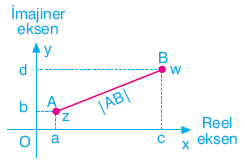
z sayısına karşılık gelen nokta A, w sayısına karşılık gelen nokta B olsun. Buna göre,
![]()
Kural
| z, değişen değerler alan bir karmaşık sayı; w sabit bir karmaşık sayı ve r, pozitif reel sayı olmak koşuluyla |z – w| = reşitliğini gerçekleyen z noktalarının kümesi, karmaşık düzlemde, merkezi w ye karşılık gelen nokta ve yarıçapı r olan bir çember belirtir.|z – w| < reşitsizliğini gerçekleyen z noktalarının kümesi, karmaşık düzlemde, merkezi w ye karşılık gelen nokta ve yarıçapı r olan çemberin iç bölgesini belirtir. |
II. KARMAŞIK SAYILARIN KUTUPSAL (TRİGONOMETRİK) GÖSTERİMİ
i2 = –1 olmak üzere, z = a + bi olsun.
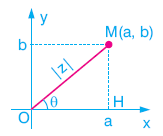
z nin karmaşık düzlemdeki görüntüsü M(a, b) noktasıdır. z karmaşık sayısını orijine birleştiren doğrunun reel eksenle (Ox ekseniyle) pozitif yönde yaptığı açıya, z karmaşık sayısının argümenti denir ve
arg(z) ile gösterilir.
![]() olsun. Bu durumda,
olsun. Bu durumda,
![]() şeklinde gösterilir.
şeklinde gösterilir.![]()
Açının esas ölçüsü olan değere de ![]() esas argüment denir. Bu durumda esas argüment; negatif olmayan ve 360° den (
esas argüment denir. Bu durumda esas argüment; negatif olmayan ve 360° den (![]() radyandan) küçük bir değerdir.
radyandan) küçük bir değerdir.
Yukarıdaki şekilde, OHM dik üçgeninden,
yazılır. Buradan,
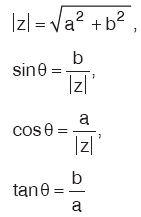
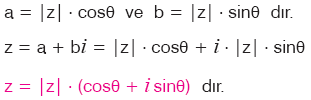
Sonuç
| i2 = –1 olmak üzere, z = a + bi olsun. z nin, mutlak değeri (orijine uzaklığı) |z| = r ve esas argümenti q olmak üzere, z = |z| × (cosq + isinq)biçiminde yazılmasına, z karmaşık sayının kutupsal (trigonometrik) gösterimi denir.z = |z| × (cosq + isinq) ifadesi z = r × cisq biçiminde kısaca gösterilebilir. |
Tanım
| i2 = –1 olmak üzere, z = a + bi olsun. Karmaşık sayının mutlak değeri ile argümentinden oluşan sıralı ikiliye bu sayının kutupsal koordinatları denir. z nin kutupsal koordinatları (|z|, q) veya (r, q) biçiminde gösterilir. |
Kural
| |
Kural
 Buna göre, iki karmaşık sayının bölümünün argümenti, bu sayıların argümentleri farkına eşittir. Bu durumda, arg(z : w) = arg(z) – arg (w) Buna göre, iki karmaşık sayının bölümünün argümenti, bu sayıların argümentleri farkına eşittir. Bu durumda, arg(z : w) = arg(z) – arg (w) |
Kural
 |
Sonuç
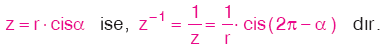 Buna göre, bir karmaşık sayının esas argümentinin ölçüsü radyan türünden a ise, bu karmaşık sayının eşleniğinin esas argümenti 2p – a dır. Buna göre, bir karmaşık sayının esas argümentinin ölçüsü radyan türünden a ise, bu karmaşık sayının eşleniğinin esas argümenti 2p – a dır. |
Sonuç
![]()
Kural
z0 = a + bi karmaşık sayısının karmaşık düzlemdeki görüntüsü M(a, b) noktası olsun. arg(z – z0) = qkoşulunu sağlayan z karmaşık sayılarının görüntüsü MP yarı doğrusudur.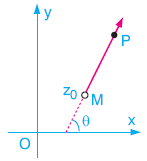 |
A. ORİJİN ETRAFINDA DÖNDÜRME
z = r × cisq karmaşık sayısının orijin etrafında pozitif yönde a kadar döndürülmesiyle elde edilen karmaşık sayı, v = r ×cis(q + a) olur. Bu durum,
v = z × (cosa + isina)
biçiminde de ifade edilebilir.
Uyarı
| Bir karmaşık sayıyı negatif yönde q derece kadar döndürmek, o sayıyı pozitif yönde 360° – q kadar döndürmektir. |
B. BİR KARMAŞIK SAYININ KÖKLERİ
![]() olmak üzere,
olmak üzere,
zn = u denklemini sağlayan z sayısına u sayısının n inci kuvvetten kökü denir.
![]()
Sonuç
| z2 = w eşitliğini sağlayan z sayıları birbirinin toplama işlemine göre tersidir. Yani, z2 = w eşitliğini sağlayan z sayıları z1 ile z2 ise,z1 = –z2 dir. |
Kural
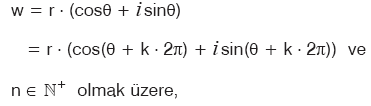 zn = w denkleminin kökleri aşağıdaki eşitliği sağlayan zk sayısında k yerine, 0, 1, 2, … , (n – 1) yazılarak bulunur. zn = w denkleminin kökleri aşağıdaki eşitliği sağlayan zk sayısında k yerine, 0, 1, 2, … , (n – 1) yazılarak bulunur.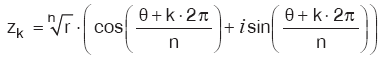 |
- Matematik Karmaşık Sayılar Çözümlü soruları izlemek ve Karmaşık Sayılar İle İlgili Önemli Formüllere Ulaşmak İçin Tıklayınız
- LYS Matematik konu Anlatımları ve Çözümlü Sorular (MAT 2) için Tıklayınız
- Tüm LYS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm YGS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
Burada bulunan Matematik Karmaşık Sayılar Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]

















