İşçi Havuz Problemleri Çözümlü Sorular ve Formüller

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik İşçi Havuz Problemleri online soru çözümleri yapan gözde hocaların İşçi Havuz Problemleri çözümlü sorular videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak anlatım yapanlara göre derleyerek aşağıya matematik İşçi Havuz Problemleri cevaplı sorular videolarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için istersenizde YGS LYS için olan online matematik İşçi Havuz Problemleri online çözümlü örnekleri istediğiniz hocayı seçerek izleyebilirsiniz. Ayrıca Videoların devamında da matematik İşçi Havuz Problemleri formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Soru Çözüm videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)
Matematik İŞÇİ HAVUZ PROBLEMLERİ Çözümlü Sorular 2 MatAkademi
Matematik İŞÇİ HAVUZ PROBLEMLERİ Çözümlü Sorular 3 MatAkademi
Matematik İŞÇİ HAVUZ PROBLEMLERİ Çözümlü Sorular 4 MatAkademi
Matematik İŞÇİ HAVUZ PROBLEMLERİ Çözümlü Sorular 2 Bugra Hoca
[t2]
Sitemizde Aşağıda yer alan Matematik İşçi Havuz Problemleri soru çözümleri gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik İşçi Havuz Problemleri canlı çözümlü örneklerin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır.
Matematik İŞÇİ HAVUZ PROBLEMLERİ Formüller ve Çözümlü Sorular
Bir işi;
A işçisi tek başına a saatte,
B işçisi tek başına b saatte,
C işçisi tek başına c saatte
yapabiliyorsa;
- A işçisi 1 saatte işin
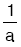 sını bitirir.
sını bitirir. - A ile B birlikte t saatte işin
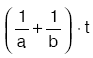 sini bitirir.
sini bitirir. - A, B, C birlikte t saatte işin
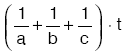 sini bitirir.
sini bitirir.
Eğer üçü t saatte işi bitirmiş ise bu ifade 1 e eşittir.
- A işçisi x saat, B işçisi y saat C işçisi z saat çalışarak işi bitiriyorsa,
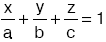 dir.
dir.
| Havuz problemleri işçi problemleri gibi çözülür. |
| A musluğu havuzun tamamını a saatte doldurabiliyor.Tabanda bulunan B musluğu dolu havuzun tamamını tek başına b saatte boşaltabiliyor olsun.
Bu iki musluk birlikte bu havuzun t saatte
|
- A musluğu havuzun tamamını a saatte doldurabiliyor. Tabanda bulunan B musluğu dolu havuzun tamamını tek başına b saatte boşaltabiliyor ise, bu iki musluk aynı anda açıldığında bu havuzun dolması için b > a olmalıdır
Soru 1
Bir isin/havuzun tamamını sırasıyla tek baslarına a, b, c günde bitirebilen/ doldurabilen A, B, C isçileri/muslukları sırasıyla x, y, z gün çalısırlarsa/akarlarsa, isin/havuzun ne kadarı bitmis/dolmus olur?
Çözüm:
Böyle bir soruda ilk basta basrol oyuncularının (bunlar isçi de olabilir, musluk da) kaçar gün çalıstıklarını kenara (bilgi yelpazesi.net) not edeceğiz.
Bu soruda zaten bu x, y, z olarak verilmis.
Ama dediğim gibi 2 gün sonra B isçisi ayrıldı, onun yerine C isçisi girdi (veya B musluğu kapatılıp onun yerine C musluğu açıldı) filan deseydi, her kisinin/musluğun ayrı ayrı kaçar gün çalıstıını hesaplamak bize düsecekti.
A isçisi isin tamamını a günde bitiriyorsa 1 günde isin
’sını yapar. E, x gün çalısmıs.
O halde x günde
’sını yapar diyeceğiz.
Benzer sekilde diger isçiler de y/b’sini ve z/c’sini yaptığından isin
(x/a) + (y/b) + (z/c)
’si yapılmıs olur.
Abartmayalım ama, bu çözüm mantığı isçi ve havuz problemlerinin %70’ini çözmeye yeter.
Soru 2.
Mustafa bir isi tek basına a günde, İmran ise aynı isin 3 katını b günde yapabiliyor.
İkisi birlikte bu isin tamamını kaç günde yapabilirler?
Çözüm:
Mustafa bu isi tek basına a günde, İmran ise bu isi tek basına b/3 günde yapıyormus.
Bulduğumuz bu değerleri formülümüzde yerine koyalım.
İkisi birlikte
günde bitirirler.
Soru 3.
Burçin arkadası Sadık’la birlikte bir isin %10’unu yapıyor. Daha sonra tek basına 3 gün çalısarak kalan kısmın 1/3’ünü yapıyor. Burçin bu isin tamamını kaç günde yapabilir?
Çözüm:
Birlikte isin %10’unu yani 1/10’unu yapmıslar. Geriye isin 9/10’u kalır.
Burçin bu 9/10’luk 1/3’ünü yani 3/10’luk isi 3 günde yaptığına göre tamamını tek basına 10 günde yapar.
Soru 4.
Üç isçi bir isi tek baslarına sırayla a, b, c günde bitirebilmektedirler.
Üçü birlikte 6 günde bitirdiklerine ve a > b > c olduğuna göre asağıdakilerden hangisi a’nın alabileceği değerlerin aralığını bulunuz?
Çözüm:
Bir an için üç isçiyi esit güçte kabul edelim.
Üçü birlikte bu isi 6 günde yapıyorlarsa, her biri tek basına 18’er günde yapıyorlar demektir.
Ama bu üç isçi esit güçte değillermis.
a > b > c olduğuna göre bu isi a günde bitiren üçünden en yavas olanıdır. Çünkü en uzun sürede bitiriyor.
Digerleri ile esit güçte saydığımızda bile 18 günde bitiriyorsa, aslında 18 günden fazla günde bitiriyormus denilebilir.
Soru 5.
Harun’un çalısma hızı Enver’in çalımsa hızının 2 katıdır. Harun ise basladıktan 2 gün sonra Enver ise baslıyor. Kalan isi ikisi birlikte 4 günde bitiriyor.
Buna göre Enver bu isi tek basına kaç günde bitirir?
Çözüm:
Harun daha hızlı olduğundan Harun bu isi a günde bitiriyorsa, Enver 2a günde bitirebilir.
Harun toplam olarak 6 gün, Enver ise 4 gün çalısıyor.
olduğundan a = 8’dir.
O halde Enver bu isi tek basına 2a = 16 günde bitirebilir.
Soru 6.
Bir isi usta tek basına 20 günde, çırak ise tek basına 50 günde bitirebiliyor.
1 usta ile 10 çırak aynı isi birlikte kaç günde bitirirler?
Çözüm:
İsi bitirme süresi ile kapasite ters orantılı olduğundan 20 usta, 50 çırağa bedelmis demeliyiz.
Yani 1 usta 2,5 tane çırak eder. O halde 10 çırak 4 usta demektir.
Bu durumda 1 usta ile 10 çırak yerine 5 usta alabiliriz. 1 usta bu isi 20 günde bitiriyorsa 5 usta toplam 4 günde bitirir.
Soru 7.
Herkesin esit is yaptığı bir isçi grubuna 30 günlük is verilmistir. İsçilerin 5’i daha is baslamadan ayrılıyor.
Kalan isçiler, isi bu yüzden 45 günde bitirdiklerine göre baslangıçtaki grup kaç kisiydi?
Çözüm:
x kisinin 30 günde yapacağı isi (x – 5) kisi 45 günde yapmıs.
Adam sayısı ile isi bitirme süresi ters orantılıdır.
Bu yüzden
x.30 = (x – 5).45
denklemi kurulur ve buradan x = 15 olarak bulunur.
Soru 8.
Bir isyerinde isçi sayısı yarıya düsürülür, günlük çalısma süresi 5 katına çıkarılır ve is miktarı 2 kat arttırılırsa isi bitirme süresi kaç katına çıkar?
Çözüm:
İsçi sayısı ile isi bitirme süresi ters orantılıdır.
İsçi sayısı yarıya düsürülünce süre 2 katına çıkar. Günlük çalısma süresi 5 katına çıkarıldığından, süre 1/5’ine düser.
İs miktarı 2 kat arttırıldığından yani 3 katına çıktığından süre de 3 katına çıkar. Simdi bulunan bu sonuçları süreye uygulayacağız.
Hiç bir sey değismeseydi, isin bitme süresi t olurdu diyelim.
Simdi ((2t)/5).3 = 6t/5 oldu yani 6/5 katına çıktı.
Soru 9.
İs güçleri aynı 9 isçi birlikte bir ise baslıyorlar. Her gün 1 isçi isten çıkarak, is 4 günde tamamlanıyor.
Eğer her gün 1 isçi çıkacağına, her gün 1 isçi bunlara katılsaydı is kaç günde biterdi?
Çözüm:
Bu isçilerden bir tanesinin bir günde x birimlik is yapabildiğini farzedelim.
İlk gün 9 isçi çalıstığından 9x birimlik is yapılır, ikinci gün 8x, üçüncü gün 7x ve dördüncü gün 6x.
Demek ki, isin tamamı 9x + 8x + 7x + 6x = 30x birimlikmis.
Eğer her gün biri eklenseydi, aynı is 3 günde biterdi, çünkü 9x + 10x + 11x = 30x olur.
Soru 10.
X bir isi x günde, X ile Y birlikte b günde yapabilmektedirler. X tek basına 3 gün çalıstıktan sonra kalan isi Y tek basına t günde bitiriyorsa, t kaçtır?
Çözüm:
Y bu isi tek basına y günde bitirebilir diyelim.
İki farklı denklem elde edilir.
Bize t’yi x ve b cinsinden sorduğundan y’yi yok etmek amacıyla, ilk denklemi t ile çarpıp bundan ikincisini çıkartalım.
bt – 3b = xt – bx olduğundan bt – xt = 3b – bx olur ki buradan
bulunur.
Soru 11.
İki musluktan birincisi bir havuzu tek basına a saatte, ikincisi ise aynı havuzun 3 katı büyüklükte baska bir havuzu b saatte (bilgi yelpazesi.net) doldurabiliyor.
İkisi birlikte küçük havuzu kaç saatte doldurabilirler?
Çözüm:
İlk musluk bu havuzu tek basına a saatte, ikincisi ise tek basına b/3 saatte doldurabiliyormus.
Bulduğumuz bu değerleri formülümüzde yerine koyalım.
İkisi birlikte
saatte doldurabilirler.
Soru 12.
Bir musluk bir havuzu tek basına 4 saatte doldururken, havuzun dibinde bu havuzun tamamını tek basına 12 saatte bosaltabilen bir musluk vardır. %ki musluk birlikte açılırsa bos havuz kaç saatte dolar?
Çözüm:
Dolduran musluk 1 saatte havuzun 1/4’ünü doldurur.
Bosaltan ise 1 saatte 1/12’sini bosaltır.
O halde 1 saatte havuzun
’sı dolar.
6’da 1’i 1 saatte doluyorsa, 6’da 6’sı yani tamamı 6 saatte dolar.
Soru 13.
A musluğu havuzun tamamını 6 saatte doldurabilmektedir. Havuzun yüksekliğinin yarısında ise bu havuzun tamamını 12 saatte bosaltabilen bir musluk bulunmaktadır.
Havuz bosken iki musluk da birlikte açılırsa, havuz kaç saatte dolar
Çözüm:
Havuzdaki su seviyesi yarıya gelinceye kadar A musluğu tek basına çalısır.
B musluğu açık olsa da bosaltacak su bulamaz.
O halde A musluğu tamamını 6 saatte doldurabildiğinden yarısına kadar 3 saatte doldurur. Artık ikisi birlikte çalısmaya baslar.
İkisinin birlikte bu havuzun tamamını kaç saatte doldurabileceklerini bulacağız.
Daha sonra sadece yarısında ikisi birlikte çalısacağından bulduğumuzun yarısını alıp 3’e ekleyeceğiz.
olduğundan ikisi birlikte bu havuzu 12 saatte doldurabilirlermis.
O halde kalan yarısı doldurabilmeleri için 6 saat gerek.
Bu yüzden cevap 3 + 6 = 9.
Soru 14.
Bir havuzu bir musluk 6 saatte doldurabilirken diger bir musluk da aynı havuzu doluyken tek basına 8 saatte bosaltabilmektedir. Havuz dolmaya basladıktan 2 saat sonra bosaltan musluğun açık olduğu farkediliyor ve kapatılıyor.
Buna göre havuzun dolması ne kadar gecikmistir?
Çözüm:
Gecikme niye oldu?
Bosaltan musluk açık unutuldu diye! 2 saat boyunca dolduran musluğun doldurduklarından bosalttığı için yani.
Yani dolduran musluk durduk yere fazla çalıstı.
Peki ne kadar fazladan doldurmak zorunda kaldı?
Bosaltanın bosalttığı kadar. Bosaltan musluk 1 saatte havuzun 1/8’ini bosalttığından, 2 saatte havuzun 1/4’ünü bosaltmıstır.
O halde dolduran musluk havuzun 1/4’ünü dolduracak kadar fazladan çalıstı.
Tamamını 6 saatte doldurduğundan 1/4’üne fazladan 1,5 saat çalısmıstır.
Dolayısıyla 1,5 saatlik bir gecikme olmustur
Soru 15.
Bir havuzu tek baslarına iki musluk sırasıyla 24 ve 30 saatte doldurabiliyor. Üçüncü bir musluk da bu havuzu bosaltıyor. Üç musluk aynı anda havuz bosken açılırsa havuz 10 saatte yarısına kadar doluyor.
Üçüncü musluk havuzu, tamamı doluyken kaç saatte bosaltır?
Çözüm:
Yarısına kadar 10 saatte doluyorsa tamamı 20 saatte dolar. Bosaltan musluğun havuzun tamamını x saatte bosalttığını farzedelim.
O halde;
esitliği geçerlidir.
Buradan x = 40 bulunur.
Soru 16.
Bir havuzu 12 saatte doldurabilen bir musluğun kapasitesi %50 arttırılırsa, aynı havuzu kaç saatte doldurur?
Çözüm:
Kapasite artısı ile dolma süresi ters orantılıdır.
100 kapasite ile akarken 12 saatte doluyorsa 150 kapasite ile akarken kaç saatte dolar diye bir ters orantı kuracağız.
100.12 = 150.x esitliğinden x = 8 olur.
Soru 17.
Bir havuzu dolduran üç musluk var. A ile B muslukları birlikte bu havuzu 8 saatte, B ile C muslukları birlikte aynı havuzu 10 saatte, A ile C muslukları da birlikte 12 saatte doldurabilmektedir.
Havuz bosken üçü birlikte açılırsa, havuz kaç saatte dolar?
Çözüm
A, B, C musluklarının bu havuzu tek baslarına doldurma sürelerine sırasıyla a, b, c diyelim.
esitlikleri taraf tarafa toplanırsa, üçünün birlikte 240/37 saatte doldurabilecekleri görülür.
Bu soruda her bir musluğun ayrı ayrı bu havuzu tek baslarına kaç saatte doldurabilecekleri de sorulabilirdi.
Taraf tarafa topladığımızda elde ettiğimiz formülde yukardaki üç esitlikten istediğimizi yerine yazarak her birini ayrı ayrı bulabiliriz.
Soru 18.
Yukarıdaki sekilde görülen havuzun dibindeki B musluğu ve yarısındaki A musluğu özdestir.
Muslukların ikisi birlikte açıkken dolu havuz 12 saatte bosalıyorsa, B musluğu tek basına bu havuzu kaç saatte bosaltır?
Çözüm:
Havuzun alt yarısında tek musluk çalısırken, üst yarısında iki musluk çalısmaktadır.
O halde (bilgi yelpazesi.net) üst yarısı t saatte bosalıyorsa, alt yarısı 2t saatte bosalır. t + 2t = 3t = 12 olduğundan t = 4 olur.
B musluğu alt yarısını 8 saatte bosaltıyormus, o halde tamamını 16 saatte bosaltabilir.
Soru 19.
Bir havuzu tek basına a saatte doldurabilen bir musluktan %40’lık tuzlu-su karısımı akmaktadır. Aynı havuzu 3a saatte doldurabilen musluktan da %60’lık tuzlu-su karısımı akmaktadır.
Bu iki musluk birlikte akarak bir havuzu doldururlarsa, havuzdaki karısımın yüzde kaçı tuz olur?
Çözüm:
Havuzun hacmi 100 olsun. 75’ini ilk musluk, 25’ini ikinci musluk doldurur.
75(%40) + 25(%60) = 30 + 15 = 45
tuz olur ki bu da karısımın %45 olduğunu gösterir.
- Matematik İŞÇİ HAVUZ PROBLEMLERİ Konu Anlatımlarını izlemek ve İŞÇİ HAVUZ PROBLEMLERİ İle İlgili Yazılı konu anlatımına Ulaşmak İçin Tıklayınız
- Tüm YGS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm YGS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm LYS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
Burada bulunan Matematik İŞÇİ HAVUZ PROBLEMLERİ Çözümlü Sorular videolarından, Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizide yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]


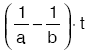 sini doldurur.
sini doldurur.














