İkinci Dereceden Denklemler Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik İkinci Dereceden Denklemler online ders anlatımı yapan gözde hocaların İkinci Dereceden Denklemler konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik İkinci Dereceden Denklemler video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik İkinci Dereceden Denklemler konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik İkinci Dereceden Denklemler konusu ile ilgili yazılı anlatım ve genel İkinci Dereceden Denklemler formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.)İkinci Dereceden Denklemler Konu Anlatımı Videolar
Matematik İkinci Dereceden Denklemler Konu Anlatımı 2 Şenol Hoca
Matematik İkinci Dereceden Denklemler Konu Anlatımı 3 Şenol Hoca
Matematik İkinci Dereceden Denklemler Konu Anlatımı 4 Şenol Hoca
Matematik İkinci Dereceden Denklemler Konu Anlatımı 2 TeknoFem
Matematik İkinci Dereceden Denklemler Konu Anlatımı 3 TeknoFem
Matematik İkinci Dereceden Denklemler Konu Anlatımı 2 MatAkademi
Matematik İkinci Dereceden Denklemler Konu Anlatımı 3 MatAkademi
Matematik İkinci Dereceden Denklemler Konu Anlatımı 4 MatAkademi
[t1]
[t2]
Sitemizde Aşağıda yer alan Matematik İkinci Dereceden Denklemler Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik İkinci Dereceden Denklemler canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.
Matematik İkinci Dereceden Denklemler Konu Anlatımı Yazılı
A. TANIM
a, b, c reel sayi ve a ¹ 0 olmak üzere,
ax2 + bx + c = 0
ifadesine x e göre düzenlenmiş ikinci dereceden bir bilinmeyenli denklem denir. Denklemi sağlayan (varsa) x reel sayilarina denklemin kökleri, tüm köklerin oluşturduğu kümeye denklemin çözüm kümesi (doğruluk kümesi), çözüm kümesini bulmak için yapilan işleme de denklem çözme denir.
B. DENKLEMiN ÇÖZÜMÜ
1. Çarpanlara Ayirma Yoluyla Denklem Çözme
ikinci dereceden denklemin çözüm kümesi, kolaylikla görülebiliyorsa, çarpanlarina ayrilarak bulunur. Bunun için,
![]() olmak üzere,
olmak üzere,
a × b = 0 ise, (a = 0 veya b = 0) olduğu göz önüne alinacaktir.
2. Formül Kullanarak Denklem Çözme
ax2 + bx + c = 0 denkleminin sol tarafi kolayca çarpanlara ayrilamayabilir. Bu durumda, ikinci dereceden bir bilinmeyenli denklemin çözümü için genel bir yaklaşima ihtiyaç vardir.
ax2 + bx + c = 0 denkleminde,
D = b2 – 4ac
ifadesine, denklemin diskiriminanti denir.
1) D > 0 ise denklemin farkli iki reel kökü vardir.
Bu kökler,
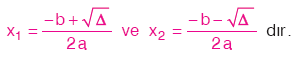
2) D = 0 ise denklemin eşit iki reel kökü vardir.
Bu kökler,
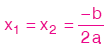
Denklemin bu köküne çift katli kök ya da çakişik kök denir.
3) D < 0 ise denklemin reel kökü yoktur. Bu durumda denklemin karmaşik iki farkli kökü vardir.
C. iKiNCi DERECEDEN BiR DENKLEME DÖNÜşEBiLEN DENKLEMLERiN ÇÖZÜMÜ
1. Polinomlarin Çarpimi Veya Bölümü şeklindeki Denklemlerin Çözümü
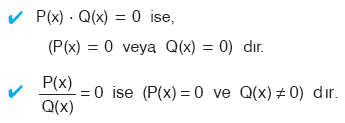
2. Yardimci Bilinmeyen Kullanilarak Çözülebilen Denklemlerin Çözümü
Verilen denklemde benzer ifadeler yeniden adlandirilarak denklem basitleştirilir. Örneğin
![]() x4 – 10x2 + 9 = 0 denkleminde x2 = t,
x4 – 10x2 + 9 = 0 denkleminde x2 = t,
![]() 22x – 6 × 2x + 8 = 0 denkleminde 2x = u,
22x – 6 × 2x + 8 = 0 denkleminde 2x = u,
![]() (x2 – 2x)2 – (x2 – 2x) – 30 = 0 denkleminde,
(x2 – 2x)2 – (x2 – 2x) – 30 = 0 denkleminde,
x2 – 2x = k,
![]()
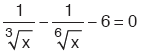 denkleminde
denkleminde ![]() adlandirilmasi yapilarak çözüme gidilir.
adlandirilmasi yapilarak çözüme gidilir.
3. Köklü Denklemlerin Çözümü
Bir denklemde bilinmeyen, kök içinde bulunuyorsa bu denkleme köklü denklem denir.
Denklemde köklü terim bir tane ise, köklü terim eşitliğin bir tarafinda yalniz birakilir. Sonra kökün derecesine göre kuvvet alinir. Gerekli işlemler yapilarak denklem çözülür. Bulunan köklerden köklü terimi tanimsiz yapmayanlar alinir.
4. Mutlak Değer içeren Denklemler
Kök içini sifir yapan değerlere göre, inceleme yapilarak çözüme gidilir. Örneğin;
![]() |x – 1| + 2x = 5 denkleminde (x £ 1 ve x >1) alinarak çözüme gidilir.
|x – 1| + 2x = 5 denkleminde (x £ 1 ve x >1) alinarak çözüme gidilir.
D. iKiNCi DERECEDEN BiR DENKLEMiN KÖKLERi iLE KAT SAYILARI ARASINDAKi BAğINTILAR
ax2 + bx + c = 0 denkleminin kökleri x1 ve x2 ise,
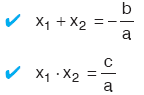
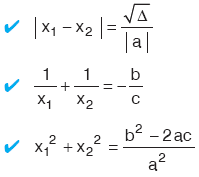
E. KÖKLERi VERiLEN iKiNCi DERECEDEN DENKLEMiN KURULUşU
Kökleri x1 ve x2 olan II. dereceden denklem;
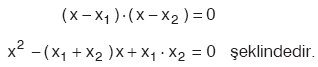
Kural
| ax2 + bx – c = 0 … |
F. ÜÇÜNCÜ DERECEDEN BiR DENKLEMiN KÖKLERi iLE KAT SAYILARI ARASINDAKi BAğINTILAR
ax3 + bx2 + cx + d = 0
denkleminin kökleri x1, x2 ve x3 ise,
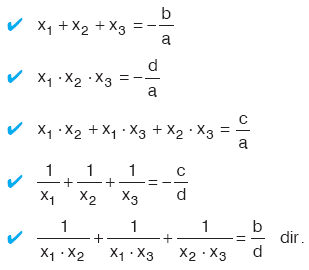
Kökleri x1, x2 ve x3 olan III. dereceden denklemin kökleri:
Aritmetik dizi oluşturuyorsa; ![]()
Geometrik dizi oluşturuyorsa; ![]()
Burada bulunan Matematik İkinci Dereceden Denklemler Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]

















