Fonksiyonlar Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Fonksiyonlar online ders anlatımı yapan gözde hocaların Fonksiyonlar konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Fonksiyonlar video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik Fonksiyonlar konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Fonksiyonlar konusu ile ilgili yazılı anlatım ve genel Fonksiyonlar formülleri de eklenmiştir.

Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen  yukarısında alt alta yer almaktadır.)Fonksiyonlar Konu Anlatımı Videolar

Sitemizde Aşağıda yer alan Matematik Fonksiyonlar Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Fonksiyonlar canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.

Matematik Fonksiyonlar Konu Anlatımı Yazılı

A. TANIM

A  ve B  olmak üzere, A dan B ye bir  bağıntısı verilmiş olsun.
A nın her elemanı B nin elemanlarıyla en az bir kez ve en çok bir kez eşleniyorsa bu bağıntıya fonksiyon denir.

x  A ve y  B olmak üzere, A dan B ye bir f fonksiyonu
f : A  B ya da x  f(x) = y biçiminde gösterilir. A ya fonksiyonun tanım kümesi, B ye de değer kümesi denir.

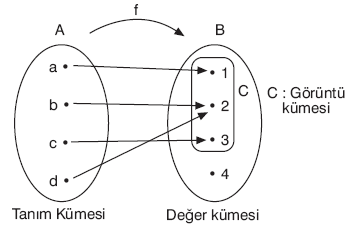
Yukarıda A dan B ye tanımlanan f fonksiyonu

f = {(a, 1), (b, 2), (c, 3), (d, 2)}

biçiminde de gösterilir.

***Her fonksiyon bir bağıntıdır. Fakat her bağıntı fonksiyon olmayabilir.

***Görüntü kümesi değer kümesinin alt kümesidir.

*** s(A) = m ve s(B) = n olmak üzere,

  i) A dan B ye n^m tane fonksiyon tanımlanabilir.

 ii) B den A ya mⁿ tane fonksiyon tanımlanabilir.

iii) A dan B ye tanımlanabilen fonksiyon olmayan bağıntıların sayısı 2^m  n – n^m dir.

*** Grafiği verilen bir bağıntının fonksiyon olup olmadığını anlamak için, y eksenine paralel doğrular çizilir. Bu doğrular fonksiyonun belirttiği eğride en az bir ve en çok bir noktayı kesiyorsa verilen bağıntı x ten y ye bir fonksiyondur.

B. FONKSİYONLARDA İŞLEMLER

A  B  olmak üzere,

  fonksiyonları tanımlansın.

1.    (f + g) : A  B   , (f + g)(x) = f(x) + g(x)

2.    (f – g) : A  B   , (f – g)(x) = f(x) – g(x)

3.    (f  g) : A  B   , (f  g)(x) = f(x)  g(x)

4.    x  A  B için, g(x)  0 olmak üzere,

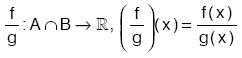
1.    c    olmak üzere,

(c  f) : A   , (c  f)(x) = c  f(x) tir.

C. FONKSİYON ÇEŞİTLERİ

1. Bire Bir Fonksiyon

Bir fonksiyonda farklı elemanların görüntüleri de farklıysa fonksiyon bire birdir.

Buna göre, bire bir fonksiyonda,

x₁, x₂  A için, x₁  x₂ iken f(x₁)  f(x₂) olur.

Diğer bir ifadeyle,

x₁, x₂  A için, f(x₁) = f(x₂) iken

x₁ = x₂ ise, f  fonksiyonu bire birdir.

*** s(A) = m ve s(B) = n (n  m) olmak üzere,

A dan B ye tanımlanabilecek bire bir fonksiyonların sayısı,

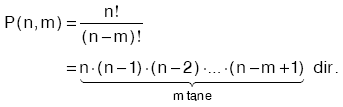
2. Örten Fonksiyon

Görüntü kümesi değer kümesine eşit olan fonksiyonlara örten fonksiyon denir.

*** f : A  B

f(A) = B ise, f örtendir.

*** s(A) = m olmak üzere, A dan A ya tanımlanabilen bire bir örten fonksiyonların sayısı,

m! = m  (m – 1)  (m – 2)  …  3  2  1 dir.

3. İçine Fonksiyon

Örten olmayan fonksiyona içine fonksiyon denir.

*** İçine fonksiyonun değer kümesinde eşlenmemiş eleman vardır.

*** s(A) = m olmak üzere, A dan A ya tanımlanabilen içine fonksiyonların sayısı m^m – m! dir.

4. Birim (Etkisiz) Fonksiyon

Her elemanı kendisine eşleyen fonksiyona birim fonksiyon denir.

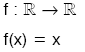
ise, f birim (etkisiz) fonksiyondur.

Birim fonksiyon genellikle I ile gösterilir.

5. Sabit Fonksiyon

Tanım kümesindeki bütün elemanları değer küme-sindeki bir elemana eşleyen fonksiyona sabit fonksiyon denir.

*** x  A ve c  B için,

      f : A  B

      f(x) = c

ise, f sabit fonksiyondur.

*** s(A) = m, s(B) = n olmak üzere,

A dan B ye n tane sabit fonksiyon tanımlanabilir.

6. Çift ve Tek Fonksiyon

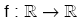
f(–x) = f(x) ise, f fonksiyonu çift fonksiyondur.

f(–x) = –f(x) ise, f fonksiyonu tek fonksiyondur.

*** Çift fonksiyonların grafikleri Oy eksenine göre simetriktir.

*** Tek fonksiyonların grafikleri orijine göre simetriktir.

D. EŞİT FONKSİYON

       f : A  B

     g : A  B

Her x  A için f(x) = g(x) ise, f fonksiyonu g fonksiyonuna eşittir.

E. PERMÜTASYON FONKSİYON

       f : A  A

olmak üzere, f fonksiyonu bire bir ve örten ise, f fonksiyonuna permütasyon fonksiyon denir.

A = {a, b, c} olmak üzere, f : A  A

f = {(a, b), (b, c), (c, a)}

fonksiyonu permütasyon fonksiyon olup

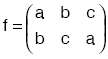biçiminde gösterilir.

 F. TERS FONKSİYON

f : A  B, f = {(x, y)|x  A, y  B} bire bir ve örten fonksiyon olmak üzere,

f^–1 : B  A, f^–1 = {(y, x)|(x, y)  f} fonksiyonuna f nin ters fonksiyonu denir.

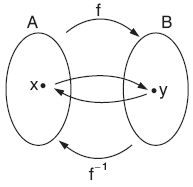
(x, y)  f ise, (y, x)  f^–1 olduğu için,

y = f(x) ise, x = f^–1(y) dir.

Ayrıca, (f^–1)^–1 = f dir.

*** (f^–1)^–1 = f dir. Ancak, (f^–1(x))^–1  f(x) tir.

*** f fonksiyonu bire bir ve örten değilse, f^–1 fonksiyon değildir.

 *** f : A  B ise, f^–1 : B  A olduğu için, f nin tanım kümesi, f^–1 in değer kümesidir. f nin değer kümesi de, f^–1 in tanım kümesidir.

*** f(a) = b ise, f^–1(b) = a dır.

f^–1(b) = a ise, f(a) = b dir.

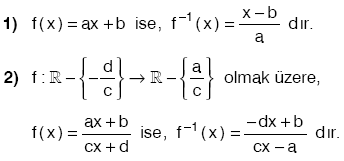
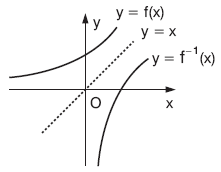
*** y = f(x) fonksiyonunun grafiği ile y = f^–1(x) in grafiği
y = x doğrusuna göre birbirinin simetriğidir

.

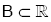***  olmak üzere, 

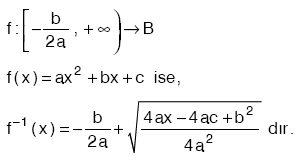
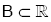***  olmak üzere,

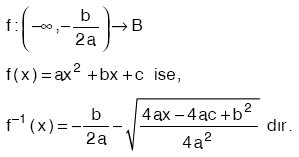
G. BİLEŞKE FONKSİYON

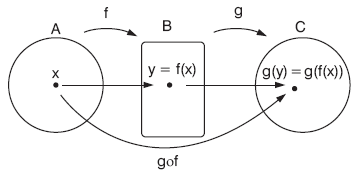
f : A  B, g : B  C fonksiyonları tanımlansın.

f ve g yi kullanarak A kümesinin elemanlarını C kümesinin elemanlarına eşleyen fonksiyona g ile f nin bileşke fonksiyonu denir.

Buna göre,

f : A  B ve g : B  C olmak üzere, gof : A  C fonksiyonuna f ile g nin bileşke fonksiyonu denir ve g bileşke f diye okunur.

*** (gof)(x) = g[f(x)] tir.

*** Bileşke işleminin değişme özeliği yoktur.

Bu durumda, fog  gof dir.

Bazı fonksiyonlar için fog = gof olabilir. Ancak bu “fonksiyonlarda değişme özeliği yoktur.” gerçeğini değiştirmez. 

*** Fonksiyonlarda bileşke işleminin birleşme özeliği vardır.

Bu durumda (fog)oh = fo(goh) = fogoh olur.

*** I birim fonksiyon olmak üzere,

foI = Iof = f ve

f^–1of = fof^–1 = I dır.

*** f, g ve h fonksiyonları bire bir ve örten olmak üzere,

(fog)^–1 = g^–1of^–1 ve

(fogoh)^–1 = h^–1og^–1of^–1 dir.

*** (fog)(x) = h(x)

ise, f(x) = (hog^–1)(x) dir.

ise, g(x) = (f^–1oh)(x) tir.

***

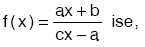
•  f^–1 (x) = f(x) tir.

•  (fof) (x) = x

•  (fofof) (x) = f(x)

•  (fofofof) (x) = x

…

H. FONKSİYONUN GRAFİĞİ

Bir fonksiyonun elemanlarına analitik düzlemde karşılık gelen noktaların kümesine bu fonksiyonun grafiği denir.

f : A  B, f = {(x, y)|x  A, y  B, y = f(x)}

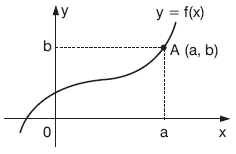
 (a, b)  f

olduğundan

f(a) = b dir.

Ayrıca, f^–1(b) = a dır.

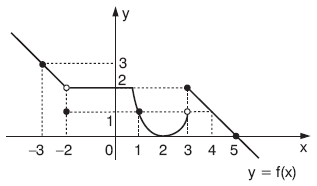
Yukarıdaki y = f(x) fonksiyonunun grafiğine göre,

f(–3) = 3, f(–2) = 1, f(–1) = 2, f(0) = 2, f(1) = 1,

f(2) = 0, f(3) = 2, f(4) = 1, f(5) = 0 dır.

Burada bulunan Matematik Fonksiyonlar Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]