Bölme ve Bölünebilme Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Bölme ve Bölünebilme online ders anlatımı yapan gözde hocaların Bölme ve Bölünebilme konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Bölme ve Bölünebilme video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik Bölme ve Bölünebilme konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Bölme ve Bölünebilme konusu ile ilgili yazılı anlatım ve genel Bölme ve Bölünebilme formülleri de eklenmiştir.

Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen  yukarısında alt alta yer almaktadır.)

Matematik Bölme ve Bölünebilme Konu Anlatımı Videolar

Sitemizde Aşağıda yer alan Matematik Bölme ve Bölünebilme Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Bölme ve Bölünebilme canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.

Matematik BÖLME VE BÖLÜNEBİLME Yazılı Konu Anlatım

A. BÖLME

A, B, C, K birer doğal sayı ve B ¹ 0 olmak üzere,

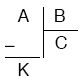
bölme işleminde,

• A ya bölünen, B ye bölen, C ye bölüm, K ya kalan denir.
• A = B × C + K dir.
• Kalan, bölenden küçüktür. (K < B)
• Kalan, bölümden (C den) küçük ise, bölen (B) ile bölümün (C) yeri değiştirilebilir. Bu durumda A ve K değişmez.
• K = 0 ise, A sayısı B ile tam bölünebilir.

B. BÖLÜNEBİLME KURALLARI

1. 2 İle Bölünebilme

Birler basamağındaki rakamı çift olan sayılar 2 ile tam bölünür.

Tek sayıların 2 ile bölümünden kalan 1 dir.

2. 3 İle Bölünebilme

Rakamlarının sayısal değerleri toplamı 3 ün katı olan sayılar 3 ile tam bölünür.

Bir sayının 3 ile bölümünden kalan, rakamlarının toplamının 3 ile bölümünden kalana eşittir.

627 = 6+2+7=15 Burada 15, 3 ile tam bölünebilmektedir ve kalan 0’dır. Dolayısıyla 627 sayısı da 3 ile tam bölünmektedir.
329= 3+2+9=14 Burada ise 14’ün 3’e bölümünden kalan 2’dir ve 329 sayısının da 3 ile bölümünden kalan 2’dir deriz.

3. 4 İle Bölünebilme

Bir sayının onlar basamağındaki rakam ile birler basamağındaki rakamın (son iki basamak) belirttiği sayı, 4 ün katı olan sayılar  ve pratik oalrak son 2 basamağı 00 olan sayılar 4 ile tam bölünür.

… abc sayısının 4 ile bölümünden kalan bc nin (son iki basamak) 4 ile bölümünden kalana eşittir.

• … abc sayısının 4 ile bölümünden kalan

c + 2 . b nin 4 ile bölümünden kalana eşittir.

4. 5 İle Bölünebilme

Birler basamağındaki rakam 0 veya 5 olan sayılar 5 ile tam bölünür.

Bir sayının 5 ile bölümünden kalan, o sayının birler basamağındaki rakamın 5 ile bölümünden kalana eşittir.

6 ile bölünebilme:

Bir sayı hem 2’ye hem de 3’e aynı anda tam olarak bölünebiliyorsa bu sayı 6 ile tam bölünebilir.

Buradaki mantık 6’nın çarpanlarıdır. Eğer 6’nın çarpanlarını oluşturan sayılara bölünebiliyorsa (2.3) 6’ya da bölünmektedir.
18, 1026, 990 gibi sayılar aynı anda hem 2 hem de 3’e tam bölünebildiği için 6’ya tam bölünebilmektedir.

5. 7 İle Bölünebilme

(n + 1) basamaklı a_na_n-1 … a₄a₃a₂a₁a₀ sayısının 7 ile tam bölünebilmesi için,

 olmak üzere,

(a₀ + 3a₁ + 2a₂) – (a₃ + 3a₄ + 2a₅) +…– … = 7k

olmalıdır.

6. 8 İle Bölünebilme

Yüzler basamağındaki, onlar basamağındaki ve birler basamağındaki rakamların (son üç rakamın) belirttiği sayı 8 in katı olan sayılar 8 ile tam bölünür.

3000, 3432, 65104 sayıları 8 ile tam bölünür.

1000, 29000, 6048 gibi sayıların son 3 hanesi 000 ya da 8’e bölünebilir olduğundan bu sayılar da 8’e tam bölünür.

7. 9 İle Bölünebilme

Rakamlarının toplamı 9 un katı olan sayılar 9 ile tam bölünür.

Bir sayının 9 ile bölümünden kalan, o sayının rakamlarının toplamının 9 ile bölümünden kalana eşittir.

2655=2+6+5+5=18 Burada 18, 9 ile tam bölündüğünden 2655 sayısı da 9’a tam bölünür.

3620=3+6+2+0=12 Burada 12’nin 9 ile bölümünden kalan 3’tür. Dolayısıyla 3620 sayısının 9 ile bölümünden kalan da 3’tür.

8. 10 İle Bölünebilme

Birler basamağındaki rakamı 0 (sıfır) olan sayılar 10 ile tam bölünebilir. Bir sayının birler basamağındaki rakam o sayının 10 ile bölümünden kalandır.

180,2030 gibi sayılar 10 ile tam bölünür.

1923 sayısının 10 ile bölümünden kalanı son rakamı olduğu gibi 3’tür.

9. 11 İle Bölünebilme

(n + 1) basamaklı a_na_{n–1 …} a₄a₃a₂a₁a₀ sayısının 11 ile tam bölünebilmesi için

(a₀ + a₂ + a₄ + …) – (a₁ + a₃ + a₅ + …)… = 11 . k

ve  olmalıdır.

yani Sayının birler basamağından başlayarak her bir rakam sağdan sola sırasıyla ”+ – + – + -…”işaretleriyle işaretlenir. Daha sonra + işaretliler toplanır ve (-) işaretliler toplanır ve aralarındaki farka bakılır. Bu fark 0 ya da 11’in katı ise o sayı 11 ile tam bölünür.

C. BÖLEN KALAN İLİŞKİSİ

A, B, C, D, E, K₁, K₂ uygun koşullarda birer doğal sayı olmak üzere,

A nın C ile bölümünden kalan K₁ ve

B nin C ile bölümünden kalan K₂ olsun.

Buna göre,

• A × B nin C ile bölümünden kalan K₁ × K₂ dir.
• A + B nin C ile bölümünden kalan K₁ + K₂ dir.
• A – B nin C ile bölümünden kalan K₁ – K₂ dir.
• D × A nın C ile bölümünden kalan D × K₁ dir.
• A^E nin C ile bölümünden kalan (K₁)^E dir.

Yukarıdaki işlemlerde kalan değerler bölenden (C den) büyük ise, tekrar C ile bölünerek kalan bulunur.

D. ÇARPANLAR İLE BÖLÜM

Bir A doğal sayısı B × C ile tam bölünüyorsa A sayısı B ve C doğal sayılarıyla da bölünebilir. Fakat bu ifadenin karşıtı (A sayısı B ile ve C ile tam bölünüyorsa A sayısı B × C ile tam bölünür.) doğru olmayabilir.

• 144 sayısı 2 × 6 = 12 ile tam bölünür ve 144 sayısı 2 ile ve 6 ile de tam bölünür.
• 6 sayısı 2 ile ve 6 ile tam bölünür. Fakat 6 sayısı 2 × 6 = 12 ile tam bölünemez.

E. BİR TAM SAYININ TAM BÖLENLERİ

Bir tam sayının, asal çarpanlarının kuvvetlerinin çarpımı biçiminde yazılmasına bu sayının asal çarpanlarının kuvvetleri biçiminde yazılması denir.

a, b, c birbirinden farklı asal sayılar ve m, n, k pozitif tam sayılar olmak üzere,

A = a^m . bⁿ . c^k  olsun.

Bu durumda aşağıdakileri söyleyebiliriz:

• A yı tam bölen asal sayılar a, b, c dir.
• A sayısının pozitif tam bölenlerinin sayısı,

      (m + 1) × (n + 1) × (k + 1) dir.

• A sayısının pozitif tam bölenlerinin ters işaretlileri de negatif tam bölenidir.
• A sayısının tam sayı bölenleri sayısı,2 × (m + 1) × (n + 1) × (k + 1) dir.
• A sayısının tam sayı bölenleri toplamı 0 (sıfır) dır.
• A sayısının pozitif tam bölenlerinin toplamı,

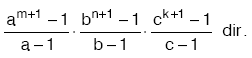
• A sayısının asal olmayan tam sayı bölenlerinin sayısı, A nın tam sayı bölenlerinin sayısından A nın asal bölenlerinin sayısı çıkarılarak bulunur.
• A nın asal olmayan tam sayı bölenleri toplamı,– (a + b + c) dir.
• A sayısından küçük A ile aralarında asal olan doğal sayıların sayısı,

A sayısının pozitif tam sayı bölenlerinin çarpımı

Burada bulunan Matematik Bölme ve Bölünebilme Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]