Birinci Dereceden Denklemler Konu Anlatımı Video

YGS-LYS, KPSS gibi sınavlara hazırlanan okuyucularımıza sınavlara çalışmalarında yardımcı olmak maksadı ile İnternette çeşitli platformlar altında yer alan matematik Birinci Dereceden Denklemler online ders anlatımı yapan gözde hocaların Birinci Dereceden Denklemler konu anlatım videolarını siz değerli Eğitim-Dünyası okuyucuları için aralarından seçim yaparak konularına göre derleyerek aşağıya matematik Birinci Dereceden Denklemler video konu anlatımlarını listeledik, Değerli okuyucumuz aşağıda ister Kpss için isterseniz de YGS LYS için olan online matematik Birinci Dereceden Denklemler konu anlatımlarından istediğiniz hocayı seçerek onun anlattığı dersi izleyebilirsiniz. Ayrıca Videoların devamında da matematik Birinci Dereceden Denklemler konusu ile ilgili yazılı anlatım ve genel Birinci Dereceden Denklemler formülleri de eklenmiştir.
Videoların Yan tarafında mevcut olan hoca ların isimlerinin üstüne tıklayarak Konu ile ilgili istediğiniz Hocanın Ders Anlatım videolarını izleyebilirsiniz. (mobil olarak bağlanan okuyucularımız hocaların isimleri videonun hemen yukarısında alt alta yer almaktadır.) Birinci Dereceden Denklemler Konu Anlatımı Videolar
Matematik BİRİNCİ DERECEDEN DENKLEMLER Konu Anlatımı 2 Şenol Hoca
Matematik BİRİNCİ DERECEDEN DENKLEMLER Konu Anlatımı 2 MatAkademi
[t2]
Sitemizde Aşağıda yer alan Matematik Birinci Dereceden Denklemler Ders izle gibi birçok branş da Derslerin Konu anlatımları online ders izleyebileceğiniz şekilde çeşitli platformlardan derlenmiş bir şekilde bulunmaktadır. matematik Birinci Dereceden Denklemler canlı dersinin bulunduğu bu sayfamızın sonunda diğer ders ve branşlara ulaşabileceğiniz bağlantı adresleri de yer almaktadır. Eğitim-Dünyası.net olarak iyi dersler dileriz.
Matematik BİRİNCİ DERECEDEN DENKLEMLER Yazılı Konu Anlatım
BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER
Bu ders notumuzda YGS, KPSS, DGS, SBS ve daha bir çok sınavda karşımıza çıkan Birinci Dereceden Denklemler konusunun geniş konu anlatımını, konun önemli yerlerini bulabilirsiniz.
A. TANIM
a ve b gerçel (reel) sayılar ve a ¹ 0 olmak üzere,
ax + b = 0 eşitliğine birinci dereceden bir bilinmeyenli denklem denir.
Bu denklemi sağlayan x değerlerinedenklemin kökü, denklemin kökünün oluşturduğu kümeye denklemin çözüm kümesi denir.
B. EŞİTLİĞİN ÖZELİKLERİ
Denklem çözümünde aşağıdaki özeliklerden yararlanırız.
- Bir eşitliğin her iki tarafına aynı sayı ilave edilirse eşitlik bozulmaz.
a = b ise, a + c = b + c dir.
- Bir eşitliğin her iki tarafından aynı sayı çıkarılırsa eşitlik bozulmaz.
a = b ise, a – c = b – c dir.
- Bir eşitliğin her iki tarafı aynı sayı ile çarpılırsa eşitlik bozulmaz.
a = b ise, a × c = b × c dir.
- Bir eşitliğin her iki tarafı sıfırdan farklı aynı sayı ile bölünürse eşitlik bozulmaz.

- Bir eşitliğin her iki tarafının n. kuvveti alınırsa eşitlik bozulmaz.
a = b ise, an = bn dir.
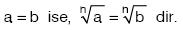
- (a = b ve b = c) ise, a = c dir.
- (a = b ve c = d) ise, a ± c = b ± d dir.
- (a = b ve c = d) ise, a × c = b × d dir.
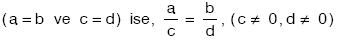 a × b = 0 ise, (a = 0 veya b = 0) dır.
a × b = 0 ise, (a = 0 veya b = 0) dır.- a × b ¹ 0 ise, (a ¹ 0 ve b ¹ 0) dır.
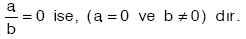
C. ax + b = 0 DENKLEMİNİN ÇÖZÜM KÜMESİ
- a ¹ 0 olmak üzere,
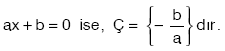
- (a = 0 ve b = 0) ise, ax + b = 0 denklemini bütün sayılar sağlar. Buna göre, reel (gerçel) sayılarda çözüm kümesi
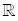 dir.
dir. - (a = 0 ve b ¹ 0) ise, ax + b = 0 denklemini sağlayan hiçbir sayı yoktur. Yani, Ç = Æ dir.
D. BİRİNCİ DERECEDEN İKİ BİLİNMEYENLİ DENKLEM SİSTEMİa, b, c Î 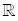 , a ¹ 0 ve b ¹ 0 olmak üzere,
, a ¹ 0 ve b ¹ 0 olmak üzere,
ax + by + c = 0 denklemine birinci dereceden iki bilinmeyenli denklem denir.
Bu denklem düzlemde bir doğru belirtir. Doğru üzerindeki bütün noktaların oluşturduğu ikililer denklemin çözüm kümesidir.
Buna göre, ax + by + c = 0 denkleminin çözüm kümesi birçok ikiliden oluşur.
a, b, c Î 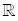 olmak üzere,ax + by + c = 0denklemi her (x, y) Î olmak üzere,ax + by + c = 0denklemi her (x, y) Î 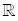 2 için sağlanıyorsaa = b = c = 0 dır. 2 için sağlanıyorsaa = b = c = 0 dır. |
Birden fazla iki bilinmeyenli denklemden oluşan sisteme birinci dereceden iki bilinmeyenli denklem sistemi denir.
Çözüm Kümesinin BulunmasıBirinci dereceden iki bilinmeyenli denklem sistemlerinin çözüm kümesi; yok etme yöntemi, yerine koyma yöntemi, karşılaştırma yöntemi, grafik yöntemi, determinant yöntemi gibi yöntemlerden biri ile yapılır.
Biz burada üçünü vereceğiz.
a. Yok Etme Yöntemi: Değişkenlerden biri yok edilecek biçimde verilen denklem sistemi düzenlenir ve taraf tarafa toplanır.
| Taraf tarafa toplandığında veya çıkarıldığında (ya da bir düzenlemeden sonra) değişkenlerden biri sadeleşiyorsa “Yok etme yöntemi” kolaylık sağlar. |
b. Yerine Koyma Yöntemi: Verilen denklemlerin birinden, değişkenlerden biri çekilip diğer denklemde yerine yazılarak sonuca gidilir.
| Denklemlerin birinden, değişkenlerden biri kolayca çekilebiliyorsa, “Yerine koyma yöntemi”kolaylık sağlar. |
c. Karşılaştırma Yöntemi: Verilen denklemlerin ikisinden de aynı değişken çekilir. Denklemlerin diğer tarafları karşılaştırılır (eşitlenir).
| Her iki denklemden de aynı değişken kolayca çekilebiliyorsa, “Karşılaştırma yöntemi”kolaylık sağlar. |
| Ü | ax + by + c = 0dx + ey + f = 0 |
denklem sistemini göz önüne alalım:
Bu iki denklemin her birinin düzlemde bir doğru belirttiği göz önüne alınırsa üç durum olduğu görülür.
ax + by + c = 0
dx + ey + f = 0
denklem sisteminde,ise, bu iki doğru tek bir noktada kesişir.
Birinci durum:
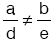
Bu durumda, verilen denklem sisteminin çözüm kümesi bir tek noktadan oluşur.
İkinci durum:ise, bu iki doğru çakışıktır.
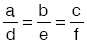
Doğru üzerindeki her nokta denklem sistemini sağlar.
Bu durumda, verilen denklem sisteminin çözüm kümesi sonsuz noktadan oluşur.
Üçüncü durum:ise, bu iki doğru paraleldir.
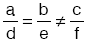
Denklem sistemini sağlayan hiçbir nokta bulunamaz.
Bu durumda, verilen denklem sisteminin çözüm kümesi boş kümedir.
- Matematik BİRİNCİ DERECEDEN DENKLEMLER Çözümlü soruları izlemek ve BİRİNCİ DERECEDEN DENKLEMLER İle İlgili Önemli Formüllere Ulaşmak İçin Tıklayınız
- Tüm YGS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Matematik konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm KPSS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm YGS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
- Tüm LYS Dersleri konu Anlatımları ve Çözümlü Sorular için Tıklayınız
Burada bulunan Matematik BİRİNCİ DERECEDEN DENKLEMLER Ders izle videolarından Açılmayan Video Dersler veya Eklenmesini istediğiniz video dersler var ise Lütfen yorum alanından bildiriniz. Ayrıca dersler ve ders anlatanlar hakkındaki soru, görüş ve önerilerinizi de yorum alanından bize iletebilirsiniz.
[egit1]
[egit2]
[egit3]

















